题目内容

∫
π
2
0
 sin2xdx=（　　）
A、0
B、
π
4
-
1
2
C、
π
4
D、
π
2
-1
考点：微积分基本定理
专题：导数的概念及应用
分析：根据微积分基本定理计算即可
解答： 解：
∫
π
2
0
 sin2xdx=
∫
π
2
0
1-cos2x
2
dx=
1
2
（x-
1
2
 sin2x）
|
π
2
0
=
1
2
（
π
2
-
1
2
sinπ-0-0）=
π
4
，
故选：C
点评：本题主要考查了微积分基本定理，关键是求出原函数．
练习册系列答案
相关题目
若不等式x2-2ax+a＞0对一切实数x∈R恒成立，则关于t的不等式at2+2t-3＜1的解集为
 
．
已知等比数列{an}中，a1=-3，a1a2a3=729
（1）求数列{an}的通项公式；
（2）设数列{
1
an
}的前n项和为Tn，证明：Tn≤-
2
9
．
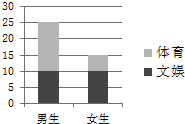对某班学生是更喜欢体育还是更喜欢文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（Ⅰ）根据图中数据，制作2×2列联表；
（Ⅱ）若要从更爱好文娱和从更爱好体育的学生中各选一人分别做文体活动协调人，求选出的两人恰好是一男一女的概率；
（Ⅲ）在多大程度上可以认为性别与是否更喜欢体育有关系？参考公式Χ2=
n(ad-bc)2
(a+c)(b+d)(a+b)(c+d)
．
参考数据：
P（K2≥k）0.500.400.250.150.100.050.0250.0100.0050.001
   k0.4550.7081.3232.0722.7063.8415.0246.6357.87910.828
已知圆心为C的圆方程是x2+y2-2y+m=0．
（1）如果圆C与直线y=0没有公共点，求实数m的取值范围；
（2）如果圆C过坐标原点，直线l过点P（0，a）（0≤a≤2），且与圆C交于A，B两点，当△ABC的面积最大时，求直线l的斜率k关于a的解析式k（a），并求k（a）的最大值．
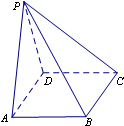如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA=PD=
2
2
AD．
（1）求证：CD⊥平面PAD；
（2）求证：平面PAB⊥平面PCD；
（3）除了已知和（2）中的两个平面互相垂直以外，在不添加其它点和线的情况下，图中还有哪些平面是互相垂直的？
为了得到函数y=cos（2x-
π
3
）的图象，可以将函数y=-sin2x的图象（　　）
A、向左平移
π
12
个单位
B、向右平移
π
12
个单位
C、向左平移
5π
12
个单位
D、向右平移
5π
12
个单位
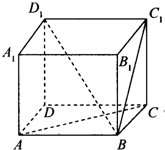在正方体ABCD-A1B1C1D1中，解答下列问题：
（1）指出直线AB与CC1的位置关系； 
（2）求直线AD与BC1所成角的大小；
（3）证明BD1⊥AC．
下列各小题中，p是q的充分必要条件的是（　　）
①p：m＜-2，或m＞6；q：x2+mx+m+3有两个不同的零点；
②p：
f(-x)
f(x)
=1；q：y=f（x）是偶函数；
③p：cosα=cosβ；q：tanα=tanβ；
④p：A∩B=A；q：∁UB⊆∁UA．
A、①②B、②③C、③④D、①④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网