题目内容
已知圆C:(x-1)2+(y-2)2=9关于直线kx-y+4=0对称.
(1)求k的值.
(2)过圆内一点P(2,1)作直线l交圆C于A、B两点,当弦AB被点P平分时,求直线l的方程.
(1)求k的值.
(2)过圆内一点P(2,1)作直线l交圆C于A、B两点,当弦AB被点P平分时,求直线l的方程.
考点:关于点、直线对称的圆的方程,直线的一般式方程
专题:计算题,直线与圆
分析:(1)由已知得圆心在直线上,代入圆心坐标,即可得到k;
(2)求出直线PC的斜率,再由两直线垂直的条件可得,所求直线l的斜率,再由点斜式方程,即可得到所求直线方程.
(2)求出直线PC的斜率,再由两直线垂直的条件可得,所求直线l的斜率,再由点斜式方程,即可得到所求直线方程.
解答:
解:(1)由已知得圆心在直线上,
将(1,2)代入直线方程得k-2+4=0,解得k=-2;
(2)因为直线PC的斜率为
=-1,
由两直线垂直的条件可得,所求直线l的斜率为1,
所以直线l的方程为:
y-1=x-2 即x-y-1=0.
将(1,2)代入直线方程得k-2+4=0,解得k=-2;
(2)因为直线PC的斜率为
| 2-1 |
| 1-2 |
由两直线垂直的条件可得,所求直线l的斜率为1,
所以直线l的方程为:
y-1=x-2 即x-y-1=0.
点评:本题考查直线与圆的方程以及位置关系,考查直线的斜率公式及运用,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各小题中,p是q的充分必要条件的是( )
①p:m<-2,或m>6;q:x2+mx+m+3有两个不同的零点;
②p:
=1;q:y=f(x)是偶函数;
③p:cosα=cosβ;q:tanα=tanβ;
④p:A∩B=A;q:∁UB⊆∁UA.
①p:m<-2,或m>6;q:x2+mx+m+3有两个不同的零点;
②p:
| f(-x) |
| f(x) |
③p:cosα=cosβ;q:tanα=tanβ;
④p:A∩B=A;q:∁UB⊆∁UA.
| A、①② | B、②③ | C、③④ | D、①④ |
某厂的产值若每年平均比上一年增长10%,经过x年后,可以增长到原来的2倍,在求x时,所列的方程正确的是( )
| A、(1+10%)x-1=2 |
| B、(1+10%)x=2 |
| C、(1+10%)x+1=2 |
| D、x=(1+10%)2 |
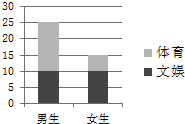 对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.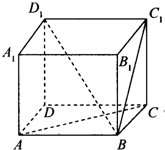 在正方体ABCD-A1B1C1D1中,解答下列问题:
在正方体ABCD-A1B1C1D1中,解答下列问题: