抛物线C:y2=2px的焦点为F.M为抛物线C上一点.若△OFM的外接圆与抛物线C的准线相切.且外接圆的面积为9π.则p=( ) A.2B.4C.6D.8 题目和参考答案——青夏教育精英家教网—

题目内容

抛物线C：y²=2px（p＞0）的焦点为F，M为抛物线C上一点，若△OFM的外接圆与抛物线C的准线相切（O为坐标原点），且外接圆的面积为9π，则p=（　　）

A、2

B、4

C、6

D、8

考点：抛物线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：根据△OFM的外接圆与抛物线C的准线相切，可得△OFM的外接圆的圆心到准线的距离等于圆的半径，由此可求p的值．

解答： 解：∵△OFM的外接圆与抛物线C的准线相切，
∴△OFM的外接圆的圆心到准线的距离等于圆的半径，
∵圆面积为9π，∴圆的半径为3，
又∵圆心在OF的垂直平分线上，|OF|=

，
∴

=3，
∴p=4
故选：B．

点评：本题考查圆与圆锥曲线的综合，考查学生的计算能力，属于基础题．

练习册系列答案

相关题目

一个几何体的三视图如图1，则该几何体的体积为

．

设f（x）是定义在R上的奇函数，当x＞0时，f（x）=x²+1，则f（-2）+f（0）=

．

甲、乙两人练习射击，命中目标的概率分别为

和

，甲、乙两人各射击一次，目标被命中的概率为（　　）

执行如图所示的程序框图，若输入n的值为8，则输出的s的值为（　　）

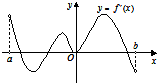函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值（　　）

已知两个平面α，β，直线l⊥α，直线m?β，有下面四个命题：
①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l⊥m⇒α∥β；④l∥m⇒α⊥β，其中正确命题有（　　）

设函数f（x）=（x-1）²+n （x∈[-1，3]，n∈N^*）的最小值为a_n，最大值为b_n，记c_n=b_n²-a_nb_n，则{c_n}是（　　）

若函数f（x）=|x²-k|的图象与函数g（x）=x-3的图象至多有一个公共点，则实数k的取值范围是（　　）

试题分类