题目内容
某省物理学会为了研究高一学生物理成绩与性别的关系,选取了一次模拟考试中某班级的30名男生和20名女生的物理成绩,并整理得到如图所示的频率分布直方图,记80分以上(包含80分)为优秀,80分以下为非优秀.
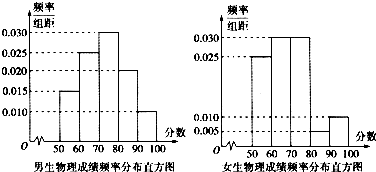
(Ⅰ)根据频率分布直方图,若按90%的可靠性要求,能否认为“成绩与性别有关系”?
(Ⅱ)从本班物理成绩为优秀的学生中任取3人,记女生的人数为随机变量X,求X的分布列和数学期望.
参考公式:K2=
参考数据:

(Ⅰ)根据频率分布直方图,若按90%的可靠性要求,能否认为“成绩与性别有关系”?
(Ⅱ)从本班物理成绩为优秀的学生中任取3人,记女生的人数为随机变量X,求X的分布列和数学期望.
参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
考点:独立性检验的应用,频率分布直方图
专题:应用题,概率与统计
分析:(Ⅰ)写出列联表,求出X2,与临界值比较,即可得到结论;
(Ⅱ)根据题意,得到变量的可能取值,结合变量对应的事件写出变量的概率,根据变量和概率的值写出分布列,做出期望值.
(Ⅱ)根据题意,得到变量的可能取值,结合变量对应的事件写出变量的概率,根据变量和概率的值写出分布列,做出期望值.
解答:
解:(Ⅰ)男生中,优秀有0.3×30=9人,非优秀有21人,女生中,优秀有0.15×20=3人,非优秀有17人.
2×2列联表
K2=
≈1.48<2.706
∴按90%的可靠性要求,不能认为“成绩与性别有关系”;
(Ⅱ)本班共有优秀12人,其中男9人,女3人,X=0,1,2,3,则
P(X=0)=
=
;P(X=1)=
=
;P(X=2)=
=
;P(X=3)=
=
;
∴X的分布列
数学期望EX=0×
+1×
+2×
+3×
=
.
2×2列联表
| 优秀 | 非优秀 | 合计 | |
| 男生 | 9 | 21 | 30 |
| 女生 | 3 | 17 | 20 |
| 合计 | 12 | 38 | 50 |
| 50×(9×17-3×21)2 |
| 30×20×12×38 |
∴按90%的可靠性要求,不能认为“成绩与性别有关系”;
(Ⅱ)本班共有优秀12人,其中男9人,女3人,X=0,1,2,3,则
P(X=0)=
| ||
|
| 21 |
| 55 |
| ||||
|
| 27 |
| 55 |
| ||||
|
| 27 |
| 220 |
| ||
|
| 1 |
| 220 |
∴X的分布列
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 21 |
| 55 |
| 27 |
| 55 |
| 27 |
| 220 |
| 1 |
| 220 |
| 3 |
| 4 |
点评:本题考查概率的计算,考查独立性检验知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
直线xcosα+ysinα+1=0,α∈(0,
)的倾斜角为( )
| π |
| 2 |
| A、α | ||
B、
| ||
| C、π-α | ||
D、
|
 如图,椭圆C:
如图,椭圆C: 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.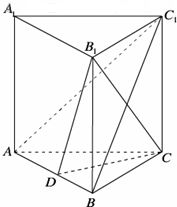 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,