题目内容
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△OAB面积取最大值时直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知设直线l的方程为y=-
x+n,由题意a=2,联立
,得(b2+9)x2-12nx+4n2-4b2=0,直线OP:x=2y,由直线OP平分线段AB解得b2=3.由此能求出椭圆C的方程.
(Ⅱ)O到直线y=-
x+n的距离d=
,|AB|=
•
,△OAB面积S=
•
,由此能求出△OAB面积取最大值时直线l的方程.
| 3 |
| 2 |
|
(Ⅱ)O到直线y=-
| 3 |
| 2 |
| |n| | ||||
|
1+
|
n2-
|
| ||
| 3 |
| 12n2-n4 |
解答:
解:(Ⅰ)由已知设直线l的方程为y=-
x+n,
由题意2a=4,解得a=2,
联立
,得(b2+9)x2-12nx+4n2-4b2=0,
△>0,设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
y1+y2=-
(x1+x2)+2n=-
+2n,
∵点P(2,1),∴直线OP:x=2y,
∵且直线OP平分线段AB,∴
=y1+y2,
即
=-
+2n,解得b2=3.
∴椭圆C的方程为
+
=1.
(Ⅱ)原点O到直线y=-
x+n的距离d=
,
x1+x2=
=n,x1x2=
=
,
|AB|=
•
=
•
,
∴△OAB面积S=
|AB|d=|n|•
=
•
,
∴当n=
时,△OAB面积S取最大值.
∴△OAB面积取最大值时直线l的方程为y=-
x+
.
| 3 |
| 2 |
由题意2a=4,解得a=2,
联立
|
△>0,设A(x1,y1),B(x2,y2),则x1+x2=
| 12n |
| b2+9 |
| 4n2-4b2 |
| b2+9 |
y1+y2=-
| 3 |
| 2 |
| 18n |
| b2+9 |
∵点P(2,1),∴直线OP:x=2y,
∵且直线OP平分线段AB,∴
| x1+x2 |
| 2 |
即
| 6n |
| b2+9 |
| 18n |
| b2+9 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)原点O到直线y=-
| 3 |
| 2 |
| |n| | ||||
|
x1+x2=
| 12n |
| b2+9 |
| 4n2-4b2 |
| b2+9 |
| n2-3 |
| 3 |
|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
1+
|
n2-
|
∴△OAB面积S=
| 1 |
| 2 |
n2-
|
=
| ||
| 3 |
| 12n2-n4 |
∴当n=
| 6 |
∴△OAB面积取最大值时直线l的方程为y=-
| 3 |
| 2 |
| 6 |
点评:本题考查椭圆方程的求法,考查三角形面积最大时直线方程的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知集合A={x∈N|0<x<3},B={x|x-1>0},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
函数y=lgx2的单调减区间为( )
| A、R |
| B、(-∞,0),(0,+∞) |
| C、(-∞,0) |
| D、(0,+∞) |

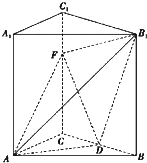 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点. 如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.