题目内容
2014年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费、养路费及汽车油费共0.7万元,
汽车维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费用均比上一年增加0.2万元
(1)设该辆轿车使用n年的总费用(包括购买费用,保险费,养路费,汽车费及维修费)为f(n),求f(n)的表达式.
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
汽车维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费用均比上一年增加0.2万元
(1)设该辆轿车使用n年的总费用(包括购买费用,保险费,养路费,汽车费及维修费)为f(n),求f(n)的表达式.
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
考点:数列与函数的综合
专题:等差数列与等比数列
分析:(1)由已知中某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.7万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,…,依等差数列逐年递增,根据等差数列前n项和公式,即可得到f(n)的表达式;
(2)由(1)中使用n年该车的总费用,得到n年平均费用表达式,根据基本不等式,计算出平均费用最小时的n值,进而得到结论.
(2)由(1)中使用n年该车的总费用,得到n年平均费用表达式,根据基本不等式,计算出平均费用最小时的n值,进而得到结论.
解答:
解:(1)由题意得:每年的维修费构成一等差数列,n年的维修总费用为
n=0.1n2-0.1n(万元)…(3分)
所以f(n)=14.4+0.7n+(0.1n2-0.1n)
=0.1n2+0.6n+14.4(万元)…(6分)
(2)该辆轿车使用n年的年平均费用为
=
0.1n+0.6+
…(9分)
≥2
+0.6
=3(万元)…(11分)
当且仅当0.1n=
时取等号,此时n=12
答:这种汽车使用12年报废最合算.…(13分)
| [0+0.2(n-1)] |
| 2 |
所以f(n)=14.4+0.7n+(0.1n2-0.1n)
=0.1n2+0.6n+14.4(万元)…(6分)
(2)该辆轿车使用n年的年平均费用为
| f(n) |
| n |
| 0.1n2+0.6n+14.4 |
| n |
0.1n+0.6+
| 14.4 |
| n |
≥2
0.1n×
|
=3(万元)…(11分)
当且仅当0.1n=
| 14.4 |
| n |
答:这种汽车使用12年报废最合算.…(13分)
点评:本题考查的知识点是根据实际问题选择函数类型,基本不等式在最值问题中的应用,数列的应用,其中(1)的关键是由等差数列前n项和公式,得到f(n)的表达式,(2)的关键是根据基本不等式,得到函数的最小值点.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
函数y=lgx2的单调减区间为( )
| A、R |
| B、(-∞,0),(0,+∞) |
| C、(-∞,0) |
| D、(0,+∞) |
 如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
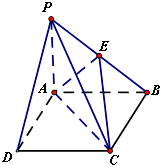 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点, 如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD.
如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD.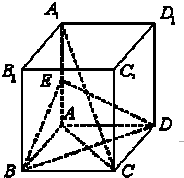 如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.