题目内容
已知函数f(x)=
,数列{an}满足a1=1,an+1=f(
)
(1)求数列{an}的通项公式;
(2)令bn=
,求数列{bn}的前n项和Tn.
| 2x+3 |
| 3x |
| 1 |
| an |
(1)求数列{an}的通项公式;
(2)令bn=
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)an+1=
=
=an+
,所以an+1-an=
,由此能求出an=
n+
.
(2)bn=
=
(
-
),由此利用裂项求和法能求出数列{bn}的前n项和Tn.
| ||
|
| 2+3an |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(2)bn=
| 1 |
| anan+1 |
| 9 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
解答:
解:(1)∵f(x)=
,数列{an}满足a1=1,an+1=f(
),
∴an+1=
=
=an+
,
∴an+1-an=
,
∴数列{an}是以
为公差,首项a1=1的等差数列,
∴an=
n+
.
(2)bn=
=
=
=
(
-
),
∴Tn=
(
-
+
-
+…+
-
)
=
(
-
)=
-
.
| 2x+3 |
| 3x |
| 1 |
| an |
∴an+1=
| ||
|
| 2+3an |
| 3 |
| 2 |
| 3 |
∴an+1-an=
| 2 |
| 3 |
∴数列{an}是以
| 2 |
| 3 |
∴an=
| 2 |
| 3 |
| 1 |
| 3 |
(2)bn=
| 1 |
| anan+1 |
| 1 | ||||||
(
|
=
| 9 |
| (2n+1)(2n+3) |
| 9 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
∴Tn=
| 9 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
=
| 9 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
| 3 |
| 2 |
| 9 |
| 4n+6 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
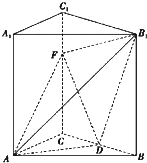 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点. 如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
 如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD.
如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD. 如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2
如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2