题目内容
已知△ABC的三内角A,B,C所对边的长分别为a,b,c,设向量
=(3c-b,a-b),
=(3a+3b,c),
∥
.
(1)求cosA的值;
(2)求sin(2A+30°)的值.
| m |
| n |
| m |
| n |
(1)求cosA的值;
(2)求sin(2A+30°)的值.
考点:两角和与差的正弦函数,平面向量共线(平行)的坐标表示,两角和与差的余弦函数
专题:三角函数的求值,解三角形
分析:(1)利用向量的数量积的坐标运算与余弦定理可求得cosA的值;
(2)利用倍角公式与两角和的正弦即可求得sin(2A+30°)的值.
(2)利用倍角公式与两角和的正弦即可求得sin(2A+30°)的值.
解答:
解:(1)∵(3c-b)c-(a-b)(3a+3b)=0,
∴a2=b2+c2-
bc,
又由余弦定理得:a2=b2+c2-2bccosA,
∴cosA=
;
(2)由cosA=
,A为△ABC的内角得:sinA=
=
,
∴sin2A=2sinAcosA=
,cos2A=2cos2A-1=-
,
∴sin(2A+30°)=sin2Acos30°+cos2Asin30°
=
×
+(-
)×
=
.
∴a2=b2+c2-
| 1 |
| 3 |
又由余弦定理得:a2=b2+c2-2bccosA,
∴cosA=
| 1 |
| 6 |
(2)由cosA=
| 1 |
| 6 |
| 1-cos2A |
| ||
| 6 |
∴sin2A=2sinAcosA=
| ||
| 18 |
| 17 |
| 18 |
∴sin(2A+30°)=sin2Acos30°+cos2Asin30°
=
| ||
| 6 |
| ||
| 2 |
| 17 |
| 18 |
| 1 |
| 2 |
3
| ||
| 36 |
点评:本题考查解三角形,考查向量的数量积的坐标运算与余弦定理.突出考查倍角公式与两角和的正弦的综合应用,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
命题“?x∈R,x2+2x+3
≥0”的否定为( )
| 2 |
A、?x0∈R,x02+2x0+3
| ||
B、?x0∈R,x02+2x0+3
| ||
C、?x∈R,x2+2x+3
| ||
D、?x∈R,x2+2x+3
|
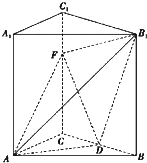 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
 如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD.
如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD.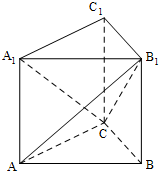 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB=