题目内容
已知函数f(x)=2
sin(ωx+
)•cos(ωx+
)-sin(2ωx+π)(ω>0),且函数f(x)的最小正周期为π.
(1)求函数f(x)的解析式;
(2)若将函数f(x)的图象向右平移
个单位长度,得到函数g(x)的图象,求函数g(x)在区间[0,
]上的最大值和最小值,并指出此时x的值.
| 3 |
| π |
| 4 |
| π |
| 4 |
(1)求函数f(x)的解析式;
(2)若将函数f(x)的图象向右平移
| π |
| 3 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)利用三角恒等变换化简函数解析式为f(x)=2sin(2ωx+
),再根据的最小正周期为π,求得ω的值,可得f(x)的解析式.
(2)根据函数y=Asin(ωx+φ)的图象变换规律,可得函数g(x)=2sin(2ωx-
),再由x∈[0,
],利用正弦函数的定义域和值域求得g(x)的最大值和最小值,并指出此时x的值.
| π |
| 3 |
(2)根据函数y=Asin(ωx+φ)的图象变换规律,可得函数g(x)=2sin(2ωx-
| π |
| 3 |
| π |
| 2 |
解答:
解:(1)∵函数f(x)=2
sin(ωx+
)•cos(ωx+
)-sin(2ωx+π)
=
sin(2ωx+
)+sin2ωx=
cos2ωx+sin2ωx=2sin(2ωx+
)的最小正周期为π,
∴
=π,解得ω=1,∴f(x)=2sin(2ωx+
).
(2)将函数f(x)的图象向右平移
个单位长度,
得到函数g(x)=2sin[2(x-
)+
]=2sin(2ωx-
)的图象,
由x∈[0,
],可得2x-
∈[-
,
],
故当2x-
=-
,即当x=0时,函数g(x)取得最小值为-
;
当2x-
=
,即当x=
时,函数g(x)取得最大值为 2.
| 3 |
| π |
| 4 |
| π |
| 4 |
=
| 3 |
| π |
| 2 |
| 3 |
| π |
| 3 |
∴
| 2π |
| 2ω |
| π |
| 3 |
(2)将函数f(x)的图象向右平移
| π |
| 3 |
得到函数g(x)=2sin[2(x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
由x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
故当2x-
| π |
| 3 |
| π |
| 3 |
| 3 |
当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,三角恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
下列结论中,正确的是( )
| A、若a>b,则a2>b2 |
| B、若a>b,c>d,则ac>bd |
| C、若a-c>a-d,则c>d |
| D、若a>b,则a(c2+1)>b(c2+1) |

 如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.
如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.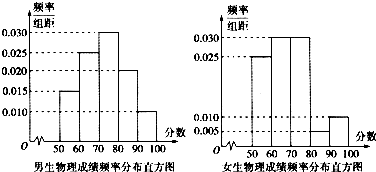
 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,
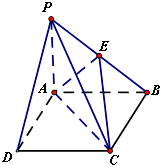
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点, 如图,在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=
如图,在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=