题目内容
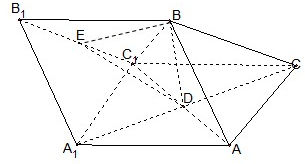 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.(1)求证:BD⊥平面AA1C1;
(2)(文)设点E是直线B1C1上一点,且DE∥平面AA1B1B,求四棱锥E-AA1C1C的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)由平行四边形AA1C1C中AC=A1C1,结合题意证出△AA1C1为等边三角形,同理得△ABC1是等边三角形,从而得到中线BD⊥AC1,利用面面垂直判定定理即可证出BD⊥平面AA1C1C.
(2)确定点E是B1C1的中点,求出BD,利用体积公式,即可求四棱锥E-AA1C1C的体积.
(2)确定点E是B1C1的中点,求出BD,利用体积公式,即可求四棱锥E-AA1C1C的体积.
解答:
(1)证明:因为四边形AA1C1C为平行四边形,所以AC=A1C1
因为AC=AA1,所以AA1=A1C1,
因为∠AA1C1=60°,所以△AA1C1为等边三角形,
同理△ABC1是等边三角形,
因为D为AC1的中点,所以BD⊥AC1,
因为平面ABC1⊥平面AA1C1C,平面ABC1∩平面AA1C1C=AC1,BD?平面ABC1,
所以BD⊥平面AA1C1C.
(2)解:设点F是A1C1的中点,因为点D是AC1的中点,所以DF∥平面AA1B1B,
又因为DE∥平面AA1B1B,
所以平面DEF∥平面AA1B1B,
又平面DEF∩平面A1B1C1=EF,
平面AA1B1B∩平面A1B1C1=A1B1,
所以EF∥A1B1,
所以点E是B1C1的中点.
由已知可得AC1=2,从而BD=
,
所以四棱锥E-AA1C1C的体积VE-AA1C1C=
VB1-AA1C1C=
VB-AA1C1C=
×
×2×2sin60°×
=
因为AC=AA1,所以AA1=A1C1,
因为∠AA1C1=60°,所以△AA1C1为等边三角形,
同理△ABC1是等边三角形,
因为D为AC1的中点,所以BD⊥AC1,
因为平面ABC1⊥平面AA1C1C,平面ABC1∩平面AA1C1C=AC1,BD?平面ABC1,
所以BD⊥平面AA1C1C.
(2)解:设点F是A1C1的中点,因为点D是AC1的中点,所以DF∥平面AA1B1B,
又因为DE∥平面AA1B1B,
所以平面DEF∥平面AA1B1B,
又平面DEF∩平面A1B1C1=EF,
平面AA1B1B∩平面A1B1C1=A1B1,
所以EF∥A1B1,
所以点E是B1C1的中点.
由已知可得AC1=2,从而BD=
| 3 |
所以四棱锥E-AA1C1C的体积VE-AA1C1C=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题考查直线与平面垂直的证明,四棱锥E-AA1C1C的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD.
如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD. 如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2
如图,P是圆O外的一点,PA为切线,A为切点,割线PBC经过圆心O,PC=6,PA=2