题目内容
19.已知数列{an},{bn}中,a1=1,an+1-(n+1)an=0,${b_1}^3+{b_2}^3+…+{b_n}^3={({{b_1}+{b_2}+…+{b_n}})^2}$且bn>0,n∈N*.记n的阶乘n(n-1)(n-2)…3•2•1=n!(1)求数列{an},{bn}的通项公式;
(2)若${c_n}=\frac{b_n}{{a{\;}_{n+1}}}$,求证:${c_1}+{c_2}+…+{c_n}≥\frac{n}{n+1}{\;}_{\;}{\;}_{\;}(n∈{N^*})$.
分析 (1)an+1-(n+1)an=0,通过递推即可得出an.
由${b_1}^3+{b_2}^3+…+{b_n}^3={({{b_1}+{b_2}+…+{b_n}})^2}$,${b_1}^3+{b_2}^3+…+{b_n}^3+{b_{n+1}}^3={({{b_1}+{b_2}+…+{b_n}+{b_{n+1}}})^2}$,两式作差得${b_{n+1}}^3=2({b_1}+{b_2}+…+{b_n}){b_{n+1}}+{b_{n+1}}^2$,再一次作差利用等差数列的通项公式即可得出.
(2)由(1)知${c_n}=\frac{b_n}{{a{\;}_{n+1}}}=\frac{n}{(n+1)!}=\frac{n+1-1}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!}$,利用裂项求和方法与数列的单调性即可得出.
解答 (1)解:∵an+1-(n+1)an=0,
∴an=nan-1=n(n-1)an-2=…=n(n-1)(n-2)…3•2•a1
又a1=1,∴an=n!…4分
由${b_1}^3+{b_2}^3+…+{b_n}^3={({{b_1}+{b_2}+…+{b_n}})^2}$,
${b_1}^3+{b_2}^3+…+{b_n}^3+{b_{n+1}}^3={({{b_1}+{b_2}+…+{b_n}+{b_{n+1}}})^2}$,
两式作差得${b_{n+1}}^3=2({b_1}+{b_2}+…+{b_n}){b_{n+1}}+{b_{n+1}}^2$,
$\begin{array}{l}∴{b_{n+1}}^2=2({b_1}+{b_2}+…+{b_n})+{b_{n+1}}\\∴{b_n}^2=2({b_1}+{b_2}+…+{b_{n-1}})+{b_n}{\;}_{\;}{\;}_{\;}(n≥2)\end{array}$,
两式作差得${b_{n+1}}^2-{b_n}^2={b_{n+1}}+{b_n}$,又bn>0,所以bn+1-bn=1(n≥2)…(*)
,而当n=1,2代入${b_1}^3+{b_2}^3+…+{b_n}^3={({b_1}+{b_2}+…+{b_n})^2}$且bn>0可直接求得b1=1,b2=2满足(*)
所以数列{bn}是等差数列,故bn=n…8分
(2)证明:由(1)知${c_n}=\frac{b_n}{{a{\;}_{n+1}}}=\frac{n}{(n+1)!}=\frac{n+1-1}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!}$,所以
当n=1时,${c_1}=\frac{1}{2}≥\frac{1}{1+1}$不等式成立
当n≥2时,${c_1}+{c_2}+…+{c_n}=1-\frac{1}{2!}+\frac{1}{2!}-\frac{1}{3!}+…+\frac{1}{n!}-\frac{1}{(n+1)!}=1-\frac{1}{(n+1)!}>1-\frac{1}{n+1}=\frac{n}{n+1}$
综上知${c_1}+{c_2}+…+{c_n}≥\frac{n}{n+1}{\;}_{\;}{\;}_{\;}(n∈{N^*})$….14分.
点评 本题考查了数列递推关系、等差数列的通项公式、裂项求和方法方法、数列的单调性,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{4-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
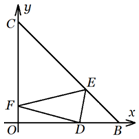 如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.
如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.