题目内容
14.已知直角坐标原点O为椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的中心,F1,F2为左右焦点,在区间(0,2)任取一个数e,则事件“以e为离心率的椭圆C与圆O:x2+y2=a2-b2没有交点”的概率为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{4-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
分析 由题意画出图形,把椭圆C与圆O:x2+y2=a2-b2没有交点转化为c<b,由此求出e的范围,再由几何概型概率计算公式求解.
解答 解:如图,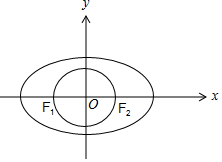
圆O:x2+y2=a2-b2=c2,
要使椭圆C与圆O:x2+y2=a2-b2没有交点,则c<b,
即c2<b2=a2-c2,
∴a2>2c2,则$\frac{{c}^{2}}{{a}^{2}}$$<\frac{1}{2}$,
∴$-\frac{\sqrt{2}}{2}<e<\frac{\sqrt{2}}{2}$,又0<e<1,
∴0$<e<\frac{\sqrt{2}}{2}$.
∴以e为离心率的椭圆C与圆O:x2+y2=a2-b2没有交点的概率P=$\frac{\frac{\sqrt{2}}{2}}{2}=\frac{\sqrt{2}}{4}$.
故选:A.
点评 本题考查椭圆的简单性质,考查数形结合的解题思想方法,训练了几何概型概率的求法,是中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
4.为了确定学生的答卷时间,需要确定回答每道题所用的时间,为此进行了5次实验,根据收集到的数据,如表所示:
由最小二乘法求得回归方程y=1.8x+a,则a的值为-0.2.
(参考公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=7}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$)
| 题数x(道) | 2 | 3 | 4 | 5 | 6 |
| 所需要时间y(分钟) | 3 | 6 | 7 | 8 | 11 |
(参考公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=7}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$)
5.若0<a<1,b>0,且${a^b}+{a^{-b}}=2\sqrt{2}$,则ab-a-b等于( )
| A. | $\sqrt{6}$ | B. | 2或-2 | C. | -2 | D. | 2 |
6.设an是${(1-\sqrt{x})^n}$的展开式中x项的系数(n=2,3,4,…),若${b_n}=\frac{{{a_{n+1}}}}{{(n+7)a_{n+2}^{\;}}}$,则bn的最大值是( )
| A. | $\frac{{9-2\sqrt{14}}}{25}$ | B. | $\frac{2}{33}$ | C. | $\frac{3}{50}$ | D. | $\frac{{7-2\sqrt{6}}}{25}$ |