题目内容
9.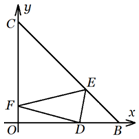 如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.
如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.
分析 根据题意,建立直角坐标系,写出对应点的坐标与直线方程,利用光的反射原理和对称性,求出点E、F的坐标,再计算|DE|、|EF|和|DF|的值,求和即可.
解答  解:建立如图所示的直角坐标系,由OB=3,BD=1,
解:建立如图所示的直角坐标系,由OB=3,BD=1,
可得B(3,0),C(0,3),D(2,0),∴BC的方程为x+y-3=0.
设M,N分别是点D关于直线BC和y轴的对称点,
则M(3,1),N(-2,0),
由光的反射原理可知,M,E,F,N四点共线,
又直线MN的方程为 $\frac{y-1}{0-1}$=$\frac{x-3}{-2-3}$,即 x-5y+2=0,
可得点E($\frac{13}{6}$,$\frac{5}{6}$),F(0,$\frac{2}{5}$),
∴|DE|=$\sqrt{{(\frac{13}{6}-2)}^{2}{+(\frac{5}{6}-0)}^{2}}$=$\frac{\sqrt{26}}{6}$,|EF|=$\sqrt{{(\frac{13}{6}-0)}^{2}{+(\frac{5}{6}-\frac{2}{5})}^{2}}$=$\frac{13\sqrt{26}}{30}$,
|DF|=$\sqrt{{(2-0)}^{2}{+(0-\frac{2}{5})}^{2}}$=$\frac{2\sqrt{26}}{5}$;
∴|DE|+|EF|+|DF|=$\sqrt{26}$,
故答案为:$\sqrt{26}$.
点评 本题考查求直线的方程,三角形的性质和轴对称图形的灵活应用问题,是中档题.

练习册系列答案
相关题目
17.“a<2”是“a2-2a<0”的( )
| A. | 充分非必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 必要非充分条件 |
14.若非零实数a,b,c满足a>b>c,则一定成立的不等式是( )
| A. | ac>bc | B. | ab>ac | C. | a-|c|>b-|c| | D. | $\frac{1}{a}<\frac{1}{b}<\frac{1}{c}$ |
6.已知$\overrightarrow a$与$\overrightarrow b$均为单位向量,它们的夹角为60°,那么$|3\overrightarrow a+2\overrightarrow b|$=( )
| A. | $\sqrt{7}$ | B. | 1 | C. | $\sqrt{19}$ | D. | 4 |