题目内容
3．已知幂函数y=f（x）的图象过点（4，2）．（1）求f（x）的解析式；
（2）画出f（x）的图象，判断它的奇偶性、单调性，并指出它的值城．
分析 （1）利用待定系数法求出函数f（x）的解析式；
（2）画出f（x）的图象，结合图象得出f（x）的奇偶性与单调性和值域．
解答 解：（1）设幂函数y=f（x）=xa，其图象过点（4，2），
∴4a=2，
解得a=$\frac{1}{2}$，
∴f（x）=${x}^{\frac{1}{2}}$=$\sqrt{x}$（x≥0）；
（2）画出f（x）的图象，如图所示：
f（x）=$\sqrt{x}$（x≥0）的定义域不关于原点对称，它既不是奇函数也不是偶函数；
函数图象从左向右上升，是增函数；
图象落在y轴以及上方，值域是[0，+∞）．
点评 本题考查了利用待定系数法求幂函数的解析式以及利用函数的图象与性质判断奇偶性、单调性和值域的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
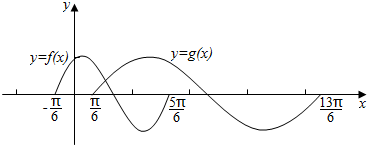
11．如图，是函数y=f（x）=sin（ω1x+φ1）和y=g（x）=sin（ω2x+φ2）在一个周期上的图象，为了得到y=f（x）的图象，只要将y=g（x）的图象上所有的点（ ）
| A． | 向左平移$\frac{π}{3}$个单位长度．再把所得点的横坐标伸长到原来的2倍．纵坐标不变 | |
| B． | 向左平移$\frac{π}{3}$个单位长度．再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍．纵坐标不变 | |
| C． | 向左平移$\frac{π}{2}$个单位长度．再把所得点的横坐标伸长到原来的2倍．纵坐标不变 | |
| D． | 向左平移$\frac{π}{2}$个单位长度．再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍．纵坐标不变 |
18．一元二次方程x2-2ix-5=0的根的情况是（ ）
| A． | 有两个不等的实根 | B． | 有一个实根和一个虚根 | ||
| C． | 有一对共轭的虚根 | D． | 有两个不共轭的虚根 |
8．在半径为R的球内放入5个球，其中有4个球大小相等，两两相外切且均与大球相内切，另一个小球与这四个球均相外切，则这个小球半径为（ ）
| A． | （3-2$\sqrt{2}$）R | B． | （4-2$\sqrt{3}$）R | C． | （5-2$\sqrt{6}$）R | D． | （6-2$\sqrt{7}$）R |
5．已知函数f（x）是定义在R上的偶函数，当x∈[0，+∞）时，f（x）是增函数，且f（-1）=0则不等式f（x）＜0的解集为（ ）
| A． | （-1，1） | B． | （-∞，-1）∪（1，+∞） | C． | （-∞，-1）∪（0，1） | D． | （-1，0）∪（0，1） |