题目内容
6.设Sn是等比数列{an}的前n项和,若a1=2a2=1,则Sn=2-($\frac{1}{2}$)n-1.分析 由题意可得数列的首项和第二项,可得公比,代入等比数列的求和公式可得.
解答 解:由题意可得等比数列{an}中a1=1,a2=$\frac{1}{2}$,
∴等比数列{an}的公比q=$\frac{1}{2}$,
∴Sn=$\frac{1×(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=2-($\frac{1}{2}$)n-1.
故答案为:2-($\frac{1}{2}$)n-1
点评 本题考查等比数列的求和公式,求出数列的首项和公比是解决问题的关键,属基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
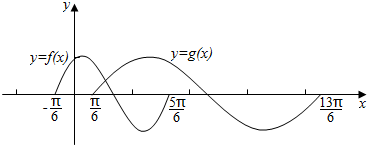
11.如图,是函数y=f(x)=sin(ω1x+φ1)和y=g(x)=sin(ω2x+φ2)在一个周期上的图象,为了得到y=f(x)的图象,只要将y=g(x)的图象上所有的点( )

| A. | 向左平移$\frac{π}{3}$个单位长度.再把所得点的横坐标伸长到原来的2倍.纵坐标不变 | |
| B. | 向左平移$\frac{π}{3}$个单位长度.再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍.纵坐标不变 | |
| C. | 向左平移$\frac{π}{2}$个单位长度.再把所得点的横坐标伸长到原来的2倍.纵坐标不变 | |
| D. | 向左平移$\frac{π}{2}$个单位长度.再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍.纵坐标不变 |
18.一元二次方程x2-2ix-5=0的根的情况是( )
| A. | 有两个不等的实根 | B. | 有一个实根和一个虚根 | ||
| C. | 有一对共轭的虚根 | D. | 有两个不共轭的虚根 |
5.已知函数f(x)是定义在R上的偶函数,当x∈[0,+∞)时,f(x)是增函数,且f(-1)=0则不等式f(x)<0的解集为( )
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(0,1) |
6.某程序框图如图所示,执行该程序,若输入的a值为1,则输出的a值为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 5 |