题目内容

若直角三角形周长为1，则它的面积的最大值是
 
．
考点：基本不等式
专题：不等式的解法及应用
分析：设直角边为a，b，则a+b+
a2+b2
=1．利用基本不等式的性质即可得出．
解答： 解：设直角边为a，b，则斜边c=
a2+b2
．
∴a+b+
a2+b2
=1．
∴1≥2
ab
+
2ab
，解得ab≤
3-2
2
2
，当且仅当a=b=
2-
2
2
时取等号．
∴S=
1
2
ab≤
3-2
2
4
．
故答案为：
3-2
2
4
．
点评：本题考查了勾股定理、基本不等式的性质，属于基础题．
练习册系列答案
相关题目
设集合A={1，3，a}，B={1，a2-a+1}，且A?B，则a的值为
 
．
若x＞0，y＞0且
2
x
+
8
y
=1，则xy的最小值是
 
．
设f（x）=
log3x(x＞0)
3x，(x＜0)
，则f[f（-3）]等于
 
．
二次函数y=x2-4的函数值组成的集合为
 
．
幂函数f（x）=xα的图象经过点（3，
1
3
），则f（x）
 
．
已知函数f（x）=（x2+x-a）e 
x
a
（a＞0）．
（1）当a=1时，求函数f（x）的单调区间；
（2）当a=5时，求f（x）的极值．
已知x，y均为非负数，且
1
x
+
3
y+2
=3，则3x+y的最小值为
 
．
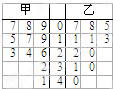某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们每场比赛得分的情况用如图所示的茎叶图表示，若甲运动员的中位数为a，乙运动员的众数为b，则a-b=（　　）
A、4B、6C、8D、12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网