题目内容
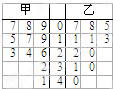某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们每场比赛得分的情况用如图所示的茎叶图表示，若甲运动员的中位数为a，乙运动员的众数为b，则a-b=（ ）| A、4 | B、6 | C、8 | D、12 |
考点：极差、方差与标准差,众数、中位数、平均数
专题：计算题,概率与统计
分析：根据给出的两组数据，把数据按照从小到大排列，根据共有11个数字，写出中位数、众数，再求差，得到结果．
解答：
解：由题意知，
∵甲运动员的得分按照从小到大排列是7，8，9，15，17，19，23，24，26，32，41，
共有11 个数字，最中间一个是19，
∴a=19；
乙运动员得分按照从小到大的顺序排列是5，7，8，11，11，13，20，22，30，31，40，
共有11个数据，出现次数最多的一个是11，
∴b=11
∴a-b=8
故选：C．
∵甲运动员的得分按照从小到大排列是7，8，9，15，17，19，23，24，26，32，41，
共有11 个数字，最中间一个是19，
∴a=19；
乙运动员得分按照从小到大的顺序排列是5，7，8，11，11，13，20，22，30，31，40，
共有11个数据，出现次数最多的一个是11，
∴b=11
∴a-b=8
故选：C．
点评：本题考查中位数，对于一组数据，通常要求的是这组数据的众数，中位数，平均数分别表示一组数据的特征，这样的问题可以出现在选择题或填空题，考查最基本的知识点．
练习册系列答案
阅读快车系列答案
相关题目
双曲线
-
=1（a，b＞0）的渐近线上任意一点P到两个焦点的距离之差的绝对值与2a的大小关系为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、恒等于2a | B、恒大于2a |
| C、恒小于2a | D、不确定 |
在1，2，3，…，9中任取2个数，有如下事件：
①恰有一个偶数和恰有一个奇数；
②至少有一个是奇数和两个数都是奇数；
③至少有一个是奇数和两个都是偶数；
④至少有一个是奇数和至少有一个是偶数．
其中互斥事件的个数是（ ）
①恰有一个偶数和恰有一个奇数；
②至少有一个是奇数和两个数都是奇数；
③至少有一个是奇数和两个都是偶数；
④至少有一个是奇数和至少有一个是偶数．
其中互斥事件的个数是（ ）
| A、1 | B、2 | C、3 | D、0 |
数列{an}和{bn}均为等差数列，a1+b1=3，a3+b3=7，则a10+b10的值为（ ）
| A、20 | B、21 | C、22 | D、23 |
已知两个不同的平面α、β和两条不重合的直线m、n，有下列四个命题：
①若m∥n，m⊥α，则n⊥α
②若m⊥α，α⊥β，则m∥β
③若m⊥α，m∥n，n?β，则α⊥β
④若m∥α，α∩β=n，则m∥n
其中正确命题的个数是（ ）
①若m∥n，m⊥α，则n⊥α
②若m⊥α，α⊥β，则m∥β
③若m⊥α，m∥n，n?β，则α⊥β
④若m∥α，α∩β=n，则m∥n
其中正确命题的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知定义域为R的奇函数f（x），当x≥0时，f（x）=|x-
|-
（a≥0），且对x∈R，恒有f（x+a）≥f（x），则实数a的取值范围是（ ）
| a |
| a |
| A、[0，2] | ||
| B、{0}∪[2，+∞） | ||
C、[0，
| ||
| D、{0}∪[16，+∞） |
定义在（0，+∞）上的函数f（x）满足对任意的x1，x2∈（0，+∞）（x1≠x2），有（x2-x1）（f（x2）-f（x1））＞0，则满足f（2x-1）＜f（
）的x的取值范围是（ ）
| 1 |
| 3 |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|