题目内容
已知正项等比数列{an}的前n项和为Sn,bn=
,且{bn}的前n项和为Tn,若对一切正整数n都有Sn>Tn,则数列{an}的公比q的取值范围是( )
| a3n |
| a2n+1 |
| A、0<q<1 | ||
| B、q>1 | ||
C、q>
| ||
D、1<q<
|
考点:数列的求和
专题:等差数列与等比数列
分析:利用等比数列的定义可得{bn}是首项为
,公比为q的等比数列,再利用等比数列求和公式求得sn和Tn,由Sn>Tn,即可求得q的取值范围.
| a1 |
| q2 |
解答:
解:设数列{an}的公比为q,且有an>0,q>0,
∴bn=
=
=a1qn-3,
∴b1=
,
=q,
∴{bn}是首项为
,公比为q的等比数列,
当q=1时,bn=an=a1,sn=Tn,与已知矛盾,∴q≠1,
∴Sn>Tn?
>
=
,
∵1-q和1-qn同号,
∴q2>1,即q>1.
故选B.
∴bn=
| a3n |
| a2n+1 |
| (a1qn-1)3 |
| (a1qn)2 |
∴b1=
| a1 |
| q2 |
| bn+1 |
| bn |
∴{bn}是首项为
| a1 |
| q2 |
当q=1时,bn=an=a1,sn=Tn,与已知矛盾,∴q≠1,
∴Sn>Tn?
| a1(1-qn) |
| 1-q |
| ||
| 1-q |
| a1(1-qn) |
| q2(1-q) |
∵1-q和1-qn同号,
∴q2>1,即q>1.
故选B.
点评:本题主要考查等比数列的定义、通项公式及求和公式等知识,考查学生的运算求解能力,属于中档题.

练习册系列答案
相关题目
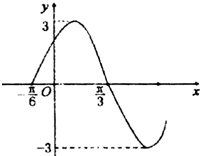
如图所示是y=Asin(ωx+φ)的图象(其中A>0,ω>0,|φ|≤
)一部分,则其解析表达式为( )
| π |
| 2 |

A、y=3cos(2x+
| ||
B、y=3cos(2x-
| ||
C、y=3sin(2x+
| ||
D、y=3sin(2x-
|
使函数y=sin(2x+θ)+
cos(2x+θ)在[-
,0]上是减函数的θ的一个值为( )
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
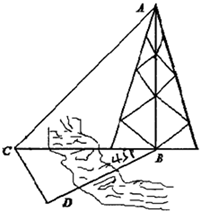 如图,测量河对岸的塔的高度AB,可以选择与B在同一水平面内的两个点C、D.测得由C望A的仰角∠ACB=45°,方位角∠BCD═60°、∠BDC=75°,又测得C、D相距20米.试求塔的高度AB.
如图,测量河对岸的塔的高度AB,可以选择与B在同一水平面内的两个点C、D.测得由C望A的仰角∠ACB=45°,方位角∠BCD═60°、∠BDC=75°,又测得C、D相距20米.试求塔的高度AB.