题目内容
使函数y=sin(2x+θ)+
cos(2x+θ)在[-
,0]上是减函数的θ的一个值为( )
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:首先根据已知将函数f(x)化简为f(x)=2sin(2x+θ+
),然后根据函数的奇偶性确定θ的取值,将选项分别代入验证再根据单调性即可排除选项.
| π |
| 3 |
解答:
解:y=sin(2x+θ)+
cos(2x+θ)=2sin(2x+θ+
),
由于函数为奇函数,
故有θ+
=kπ
即:θ=kπ-
(k∈Z),可淘汰B、C选项
然后分别将A和D选项代入检验,
易知当θ=
时,
f(x)=-2sin2x其在区间[-
,0]上递减,故选D、
故选:D.
| 3 |
| π |
| 3 |
由于函数为奇函数,
故有θ+
| π |
| 3 |
即:θ=kπ-
| π |
| 3 |
然后分别将A和D选项代入检验,
易知当θ=
| 2π |
| 3 |
f(x)=-2sin2x其在区间[-
| π |
| 4 |
故选:D.
点评:本题考查正弦函数的奇偶性和单调性,通过对已知函数的化简,判断奇偶性以及单调性,通过对选项的分析得出结果.考查了对三角函数图象问题的熟练掌握和运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正项等比数列{an}的前n项和为Sn,bn=
,且{bn}的前n项和为Tn,若对一切正整数n都有Sn>Tn,则数列{an}的公比q的取值范围是( )
| a3n |
| a2n+1 |
| A、0<q<1 | ||
| B、q>1 | ||
C、q>
| ||
D、1<q<
|
函数y=
的值域是( )
| 16-4x |
| A、[0,+∞) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
如果执行图中的程序框图,那么输出的n为( )


| A、5 | B、6 | C、7 | D、8 |
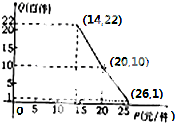 甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.
甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.