题目内容
已知实数x、y满足x∈A,y∈B,
(1)若A={0,1,2},B={0,1,2},求x+yi为虚数的概率;
(2)若A=[0,1],B=[0,1],求x、y满足不等式组
的概率.
(1)若A={0,1,2},B={0,1,2},求x+yi为虚数的概率;
(2)若A=[0,1],B=[0,1],求x、y满足不等式组
|
考点:几何概型,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)古典概型:列举可得总的基本事件共9种,其中满足x+yi为虚数的共6种,由概率公式可得;
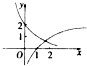
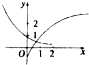
(2)几何概型:总的基本事件够成如图所示的正方形OCDE,其中满足不等式组
的为图中的阴影部分,由定积分可求得阴影的面积S可得.
(2)几何概型:总的基本事件够成如图所示的正方形OCDE,其中满足不等式组
|
解答:
 解:(1)∵x∈A={0,1,2},y∈B={0,1,2},
解:(1)∵x∈A={0,1,2},y∈B={0,1,2},
∴总的基本事件为(0,0),(0,1),(0,2),(1,0),
(1,1),(1,2),(2,0),(2,1),(2,2)共9种,
其中满足x+yi为虚数的有(0,1),(0,2),(1,1),
(1,2),(2,1),(2,2)共6种,
∴x+yi为虚数的概率P=
=
;
(2)∵x∈A=[0,1],y∈B=[0,1],
∴总的基本事件够成如图所示的正方形OCDE,
其中满足不等式组
的为图中的阴影部分,
由定积分可求得阴影的面积S=
(
-x2)dx=(
x
-
x3
=
∴x、y满足不等式组
的概率P′=
=
 解:(1)∵x∈A={0,1,2},y∈B={0,1,2},
解:(1)∵x∈A={0,1,2},y∈B={0,1,2},∴总的基本事件为(0,0),(0,1),(0,2),(1,0),
(1,1),(1,2),(2,0),(2,1),(2,2)共9种,
其中满足x+yi为虚数的有(0,1),(0,2),(1,1),
(1,2),(2,1),(2,2)共6种,
∴x+yi为虚数的概率P=
| 6 |
| 9 |
| 2 |
| 3 |
(2)∵x∈A=[0,1],y∈B=[0,1],
∴总的基本事件够成如图所示的正方形OCDE,
其中满足不等式组
|
由定积分可求得阴影的面积S=
| ∫ | 1 0 |
| x |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ) | 1 0 |
| 1 |
| 3 |
∴x、y满足不等式组
|
| ||
| 1 |
| 1 |
| 3 |
点评:本题考查古典概型和几何概型,涉及列举法和定积分求面积,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知正项等比数列{an}的前n项和为Sn,bn=
,且{bn}的前n项和为Tn,若对一切正整数n都有Sn>Tn,则数列{an}的公比q的取值范围是( )
| a3n |
| a2n+1 |
| A、0<q<1 | ||
| B、q>1 | ||
C、q>
| ||
D、1<q<
|
函数y=
的值域是( )
| 16-4x |
| A、[0,+∞) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
数列{an}的前n项和Sn=n2-9n,若5<ak<8,则k=( )
| A、6 | B、7 | C、8 | D、9 |
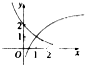
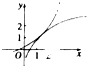
 如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:
如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求: