题目内容
已知函数f(x)=x2+mx-|1-x2|(m∈R),若f(x)在区间(-2,0)上有且只有1个零点,则实数m的取值范围是 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:通过讨论x的范围,得出函数的解析式,由f(-1)=1-m,通过讨论1-m的范围,结合函数的图象的性质,从而求出m的范围.
解答:
解:-1≤x<0时,f(x)=2x2+mx-1,
-2<x<-1时,f(x)=mx+1,
∴当x=-1时,f(-1)=1-m,
当1-m=0,即m=1时,符合题意,
当1-m>0时,f(x)在(-1,0)有零点,
∴f(-2)=-2m+1≥0,解得:m≤
,
当1-m<0,在(-2,0)上,函数与x轴无交点,
故答案为:{m|m≤
或m=1}.
-2<x<-1时,f(x)=mx+1,
∴当x=-1时,f(-1)=1-m,
当1-m=0,即m=1时,符合题意,
当1-m>0时,f(x)在(-1,0)有零点,
∴f(-2)=-2m+1≥0,解得:m≤
| 1 |
| 2 |
当1-m<0,在(-2,0)上,函数与x轴无交点,
故答案为:{m|m≤
| 1 |
| 2 |
点评:本题考查了函数零点的判定定理,考查了分段函数,考查了分类讨论思想,是一道中档题.

练习册系列答案
相关题目
某设备的使用年限x与所支出的总费用y(万元)统计数据如下表
据上表可得回归方程
=
x+
中的
=0.7,据此预测设备使用年限为6年时总费用为( )
| 使用年限x | 1 | 2 | 3 | 4 |
| 总费用y | 1.5 | 2 | 3 | 3.5 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、4.95万元 |
| B、5.2万元 |
| C、4.35万元 |
| D、4.9万元 |
已知正项等比数列{an}的前n项和为Sn,bn=
,且{bn}的前n项和为Tn,若对一切正整数n都有Sn>Tn,则数列{an}的公比q的取值范围是( )
| a3n |
| a2n+1 |
| A、0<q<1 | ||
| B、q>1 | ||
C、q>
| ||
D、1<q<
|
函数y=
的值域是( )
| 16-4x |
| A、[0,+∞) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
已知集合A={x|x2-2x<0},B={x|-
<x<
},则( )
| 5 |
| 5 |
| A、A∩B=∅ | B、A∪B=R |
| C、B⊆A | D、A⊆B |
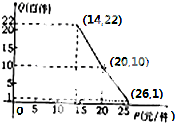 甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.
甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.