题目内容
设函数sgn(x)=
,求函数f(x)=sgn(lnx)-ln2x的零点.
|
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:函数f(x)=sgn(lnx)-ln2x的零点即方程f(x)=sgn(lnx)-ln2x=0的根,讨论求根即可.
解答:
解:①当lnx>0,即x>1时,
f(x)=sgn(lnx)-ln2x=0可化为:1-ln2x=0,
解得,x=e;
②当lnx=0,即x=1时,
f(x)=sgn(lnx)-ln2x=0可化为0-ln21=0,显然成立;
③当lnx<0,即0<x<1时,
f(x)=sgn(lnx)-ln2x=0可化为:
-1-ln2x=0,
无解;
综上所述,
x=e或x=1.
f(x)=sgn(lnx)-ln2x=0可化为:1-ln2x=0,
解得,x=e;
②当lnx=0,即x=1时,
f(x)=sgn(lnx)-ln2x=0可化为0-ln21=0,显然成立;
③当lnx<0,即0<x<1时,
f(x)=sgn(lnx)-ln2x=0可化为:
-1-ln2x=0,
无解;
综上所述,
x=e或x=1.
点评:本题考查了函数的零点与方程的根之间的关系,同时考查了分类讨论的思想,属于中档题.

练习册系列答案
相关题目
当x、y满足不等式组
时,-2≤kx-y≤2恒成立,则实数k的取值范围是( )
|
| A、[-1,-1] | ||||
| B、[-2,0] | ||||
C、[-
| ||||
D、[-
|

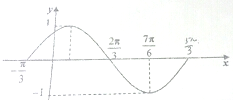 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<