题目内容
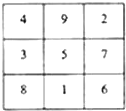我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，…，9填入3×3的方格内，使三行、三列、二对角线的三个数之和都等于15，如图所示，一般地，将连续的正整数1，2，3，…，n2填入n×n个方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记n阶幻方的对角线上数的和为N，如图的幻方记为N3=15，那么N12的值为考点：进行简单的合情推理,数列的函数特性
专题：推理和证明
分析：根据题意可知，幻方对角线上的数成等差数列，根据等差数列的性质可知对角上的两个数相加正好等于1+n2，进而根据等差数列的求和公式求得答案
解答：
解：根据题意可知，幻方对角线上的数成等差数列，
根据等差数列的性质可知对角上的两个数相加正好等于1+n2，
根据等差数列的求和公式数列的和S=
，
N12=
=870
故答案为：870
根据等差数列的性质可知对角上的两个数相加正好等于1+n2，
根据等差数列的求和公式数列的和S=
| n(n2+1) |
| 2 |
N12=
| 12(122+1) |
| 2 |
故答案为：870
点评：本题主要考查了等差数列的性质和等差数列的前n项和公式，本题解题的关键是应用等差数列的性质来解题．
练习册系列答案
相关题目
如图所示，在边长为5+下列各式错误的是（ ）
| A、30.8＞30.7 | ||||
| B、0.75-0.1＜0.750.1 | ||||
C、（
| ||||
| D、0.50.4＞0.50.6 |
已知三角形ABC的三边长a，b，c成等差数列，且a2+b2+c2=84，则实数b的取值范围
是（ ）
是（ ）
A、(0，2
| ||||
B、(2
| ||||
C、(0，2
| ||||
D、[2
|
有三个游戏规则如下，袋子中分别装有形状、大小相同的球，从袋中无放回地取球，
问其中不公平的游戏是（ ）
| 游戏1 | 游戏2 | 游戏3 |
| 袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
| 从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
| 若取出的两个球同色，则甲胜 | 若取出的两个球同色，则甲胜 | 若取出的两个球同色，则甲胜 |
| 若取出的两个球不同色，则乙胜 | 若取出的两个球不同色，则乙胜 | 若取出的两个球不同色，则乙胜 |
| A、游戏2 |
| B、游戏3 |
| C、游戏1和游戏2 |
| D、游戏1和游戏3 |
若点P（-
，m）是角θ终边上一点，且sinθ=
，则m的值为（ ）
| 3 |
| ||
| 3 |
A、
| ||||
B、±
| ||||
C、
| ||||
D、±
|