题目内容
若|x+1|+|2x+a|≥-y2+2y+2对于任意的x,y恒成立,则实数a的值为 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:这是一个不等式恒成立问题,先求出右边式子的最大值m,然后再让左边关于x的函数最小值大于或等于m即可.
解答:
解:由-y2+2y+2=-(y-1)2+3,最大值为3,所以只需|x+1|+|2x+a|≥3即可.
当-
≤-1时即a≥2时,f(x)=
,易知当x=-
时,函数取最小值f(-
)=
-1=3,所以a=8.
当-
>-1即a<2时,f(x)=
,易知当x=-
时,函数取最小值f(-
)=-
+1=3,所以a=-4.
故a的值为-4或8.
故答案为:-4或8.
当-
| a |
| 2 |
|
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
当-
| a |
| 2 |
|
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
故a的值为-4或8.
故答案为:-4或8.
点评:本题考查了含有两个绝对值符号的函数的最值问题,一般需要分类讨论求解.

练习册系列答案
相关题目
已知一组数据a1,a2,a3,…,an的平均数为
,标准差为s,则-2a1+3,-2a2+3,-2a3+3,…,-2an+3的平均数和标准差分别是( )
. |
| x |
A、
| ||
B、-2
| ||
C、-2
| ||
D、-2
|
抛物线y2=12x的焦点为( )
| A、(6,0) |
| B、(0,6) |
| C、(3,0) |
| D、(0,3) |
直线x+
y-3=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |

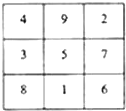 我国的《洛书》中记载着世界上最古老的一个幻方:将1,2,…,9填入3×3的方格内,使三行、三列、二对角线的三个数之和都等于15,如图所示,一般地,将连续的正整数1,2,3,…,n2填入n×n个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方,记n阶幻方的对角线上数的和为N,如图的幻方记为N3=15,那么N12的值为
我国的《洛书》中记载着世界上最古老的一个幻方:将1,2,…,9填入3×3的方格内,使三行、三列、二对角线的三个数之和都等于15,如图所示,一般地,将连续的正整数1,2,3,…,n2填入n×n个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方,记n阶幻方的对角线上数的和为N,如图的幻方记为N3=15,那么N12的值为