题目内容
已知三角形ABC的三边长a,b,c成等差数列,且a2+b2+c2=84,则实数b的取值范围
是( )
是( )
A、(0,2
| ||||
B、(2
| ||||
C、(0,2
| ||||
D、[2
|
考点:等差数列的通项公式
专题:等差数列与等比数列,解三角形
分析:由a,b,c成等差数列,设公差为d,则有a=b-d,c=b+d,代入已知等式求出b的最大值;由三角形三边关系列出不等式,整理后求出b的范围,即可确定出满足题意b的范围.
解答:
解:设公差为d,则有a=b-d,c=b+d,
代入a2+b2+c2=84化简可得3b2+2d2=84,
当d=0时,b有最大值为2
,
由三角形任意两边之和大于第三边,得到较小的两边之和大于最大边,即a+b>c,
整理得:b>2d,
∴3b2+2(
)2>84,
解得:b>2
,
则实数b的取值范围是(2
,2
].
故选:B.
代入a2+b2+c2=84化简可得3b2+2d2=84,
当d=0时,b有最大值为2
| 7 |
由三角形任意两边之和大于第三边,得到较小的两边之和大于最大边,即a+b>c,
整理得:b>2d,
∴3b2+2(
| b |
| 2 |
解得:b>2
| 6 |
则实数b的取值范围是(2
| 6 |
| 7 |
故选:B.
点评:此题考查了等差数列的性质,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
直线x+
y-3=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
在简单随机抽样中,某一个个体被抽中的可能性( )
| A、与第几次抽样有关,第1次抽中的可能性要大些 |
| B、与第几次抽样无关,每次抽中的可能性都相等 |
| C、与第几次抽样有关,最后一次抽中的可能性大些 |
| D、与第几次抽样无关,每次都是等可能的抽取,但各次抽取的可能性不一样 |
某程序框图如图所示,该程序运行后输出的s值是( )


| A、30 | B、31 | C、62 | D、63 |
在复平面内,复数
(i是虚数单位)所对应的点位于( )
| -2+3i |
| 3-4i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
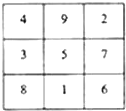 我国的《洛书》中记载着世界上最古老的一个幻方:将1,2,…,9填入3×3的方格内,使三行、三列、二对角线的三个数之和都等于15,如图所示,一般地,将连续的正整数1,2,3,…,n2填入n×n个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方,记n阶幻方的对角线上数的和为N,如图的幻方记为N3=15,那么N12的值为
我国的《洛书》中记载着世界上最古老的一个幻方:将1,2,…,9填入3×3的方格内,使三行、三列、二对角线的三个数之和都等于15,如图所示,一般地,将连续的正整数1,2,3,…,n2填入n×n个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方,记n阶幻方的对角线上数的和为N,如图的幻方记为N3=15,那么N12的值为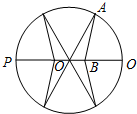 为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草.如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形OAB的顶点O为圆心,A在圆周上,B在半径OQ上,设计要求∠ABO=120°.
为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草.如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形OAB的顶点O为圆心,A在圆周上,B在半径OQ上,设计要求∠ABO=120°.