题目内容
已知曲线C1的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0,设曲线C1,C2相交于两点A,B,则过AB中点且与直线AB垂直的直线的直角标方程为( )
|
A、y=-
| ||||||||
B、y=
| ||||||||
C、y=-
| ||||||||
D、y=
|
考点:参数方程化成普通方程
专题:直线与圆,坐标系和参数方程
分析:将曲线C1的参数方程化为普通方程,运用x=ρcosθ,y=ρsinθ,将曲线C2的极坐标方程化为普通方程,求出圆心,由过AB中点且与直线AB垂直的直线必过圆心,即可求出所求直线方程.
解答:
解:曲线C1的参数方程为
(t为参数),化为普通方程为x-
y-1=0,
曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0,化为直角坐标方程为x2+y2-2x-2y+1=0,
表示圆心为(1,1),半径为1的圆,过AB中点且与直线AB垂直的直线必经过圆心,
故所求方程为y-1=-
(x-1),即y=-
x+1+
.
故选A.
|
| ||
| 3 |
曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0,化为直角坐标方程为x2+y2-2x-2y+1=0,
表示圆心为(1,1),半径为1的圆,过AB中点且与直线AB垂直的直线必经过圆心,
故所求方程为y-1=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
故选A.
点评:本题考查参数方程与普通方程的互化,极坐标方程与普通方程的互化,以及直线与圆的位置关系,两直线的位置关系,属于基础题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
使不等式sinx≥
(x∈R)成立的x的集合是( )
| ||
| 2 |
A、{x|x≥
| ||||
B、{x|2kπ+
| ||||
C、{x|
| ||||
D、{x|x≥2kπ+
|
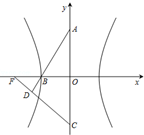 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若f(x)是定义在R上的可导函数,且满足(x-1)f′(x)≥0,则必有( )
| A、f(0)+f(2)<2f(1) |
| B、f(0)+f(2)>2f(1) |
| C、f(0)+f(2)≤2f(1) |
| D、f(0)+f(2)≥2f(1) |
已知a>3,则z=
+a的最小值是( )
| 1 |
| a-3 |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
已知双曲线C:
-
=1(a>0,b>0)的焦距为2
,若抛物线x2=16y的焦点到双曲线C的渐近线的距离为
,则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
8
| ||
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
若a>0,b>0,则p=
+
与q=a+b的大小关系为( )
| b2 |
| a |
| a2 |
| b |
| A、p>q | B、p≥q |
| C、p<q | D、p≤q |