题目内容
设函数f（x）在R上可导，其导函数为f′（x），且函数f（x）在x=-1处取得极小值，则函数y=x f′（x）的图象可能是（ ）
A、 |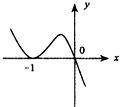
B、 |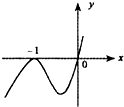
C、 |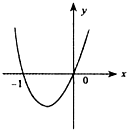
D、 |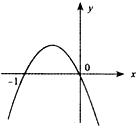
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：由函数f（x）在x=-1处取得极小值，得x＜-1时，f′（x）＜0，x＞-1时，f′（x）＞0，讨论x∈（-∞，-1）时x∈（-1，0）时x∈（0，+∞）时的情况，从而得出答案．
解答：
解：∵函数f（x）在x=-1处取得极小值，
∴x＜-1时，f′（x）＜0，x＞-1时，f′（x）＞0，
∴x∈（-∞，-1）时，y=xf′（x）＞0，
x∈（-1，0）时，y=xf′（x）＜0，
x∈（0，+∞）时，y=xf′（x）＞0，
故选：C．
∴x＜-1时，f′（x）＜0，x＞-1时，f′（x）＞0，
∴x∈（-∞，-1）时，y=xf′（x）＞0，
x∈（-1，0）时，y=xf′（x）＜0，
x∈（0，+∞）时，y=xf′（x）＞0，
故选：C．
点评：本题考查了函数的单调性，导数的应用，渗透了数形结合思想，是一道基础题．
练习册系列答案
相关题目
已知曲线C1的参数方程为
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0，设曲线C1，C2相交于两点A，B，则过AB中点且与直线AB垂直的直线的直角标方程为（ ）
|
A、y=-
| ||||||||
B、y=
| ||||||||
C、y=-
| ||||||||
D、y=
|
已知离心率为
的椭圆T：
+
=1（a＞0，b＞0）过点M（0，1），过点M引两条互相垂直的直线l1，l2，若P为椭圆上任意一点，记点P到两直线的距离分别为d1，d2，则d12+d22的最大值是（ ）
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、2 |
对于R上可导的任意函数f（x），若满足（x-3）f′（x）≥0，则必有（ ）
| A、f（0）+f（5）＜2f（3） |
| B、f（0）+f（5）≤2f（3） |
| C、f（0）+f（5）≥2f（3） |
| D、f（0）+f（5）＞2f（3） |
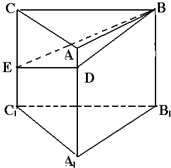如图，已知体积为8，高为4的三棱柱ABC-A1B1C1，CC1⊥平面A1B1C1，点D、E分别在棱AA1和CC1上，且DE⊥B1C1，DA1=3，EC1=2．
如图，斜三棱柱ABC-A1B1C1的所有棱长均为a，侧面B1C1CB⊥底面ABC，且AC1⊥BC．