题目内容
已知A(1,2),B(3,4),C(-2,2),D(-3,5),则向量
在向量
上的投影为 .
| CD |
| AB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:先求得向量的坐标,再求得其数量积和模,然后用投影公式求解.
解答:
解:
=(2,2)
=(-1,3),|
|=
,
•
=4,设向量
和
的夹角为α,则cosα=
,所以向量
在向量
方向上的投影为:
|
|•cosα=
=
.故答案为:
.
| AB |
| CD |
| AB |
| 8 |
| AB |
| CD |
| AB |
| CD |
| ||||
|
|
| CD |
| AB |
|
| CD |
| 4 | ||
|
| 2 |
| 2 |
点评:本题用到的知识点有:向量的坐标表示,向量用坐标求模,数量级的坐标运算,投影的定义及公式,这些都需要熟练掌握.

练习册系列答案
相关题目
已知函数f(x)=3x3-ax2+x-5在区间[1,2]上单调递减,则a的取值范围是( )
A、[5,
| ||
B、(-∞,5)∪(
| ||
| C、[5,+∞) | ||
D、[
|
已知曲线C1的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0,设曲线C1,C2相交于两点A,B,则过AB中点且与直线AB垂直的直线的直角标方程为( )
|
A、y=-
| ||||||||
B、y=
| ||||||||
C、y=-
| ||||||||
D、y=
|
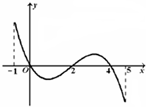 已知函数y=f(x)的定义域为[-1,5],部分对应值如下表,y=f(x)的导函数y=f′(x)的图象如图所示.下列关于y=f(x)的命题:
已知函数y=f(x)的定义域为[-1,5],部分对应值如下表,y=f(x)的导函数y=f′(x)的图象如图所示.下列关于y=f(x)的命题: