题目内容
已知a＞3，则z=
+a的最小值是（ ）
| 1 |
| a-3 |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
考点：基本不等式
专题：不等式的解法及应用
分析：利用基本不等式即可求得函数的最小值，注意等号取到的条件．
解答：
解：∵a＞3，
∴a-3＞0，
∴z=
+a=
+a-3+3≥2
+3=2+3=5，当且仅当a=4，取等号．
∴则z=
+a的最小值是5．
故选：D．
∴a-3＞0，
∴z=
| 1 |
| a-3 |
| 1 |
| a-3 |
|
∴则z=
| 1 |
| a-3 |
故选：D．
点评：该题考查利用基本不等式求函数的最值，属基础题，注意使用基本不等式的条件：一正、二定、三相等．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
在等差数列{an}中，已知ak=1，ak+1=sin2θ，则ak+2=（ ）
| A、cos2θ |
| B、-cos2θ |
| C、cos2θ |
| D、-cos2θ |
双曲线
-
=1与
-
=k始终有相同的（ ）
| x2 |
| 5 |
| y2 |
| 4 |
| x2 |
| 5 |
| y2 |
| 4 |
| A、焦点 | B、准线 |
| C、渐近线 | D、离心率 |
已知曲线C1的参数方程为
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0，设曲线C1，C2相交于两点A，B，则过AB中点且与直线AB垂直的直线的直角标方程为（ ）
|
A、y=-
| ||||||||
B、y=
| ||||||||
C、y=-
| ||||||||
D、y=
|
定义A㊣B、B㊣C、C㊣D、D㊣A的运算分别对应图中的（1）、（2）、（3）、（4）．则图中的甲、乙的运算式可以表示为：（ ）
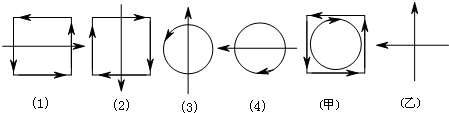
| A、B㊣D、C㊣A |
| B、B㊣D、A㊣C |
| C、D㊣B、C㊣A |
| D、D㊣B、A㊣C |
若函数f（x）=x3-
x2+1，则（ ）
| 3 |
| 2 |
A、最大值为1，最小值为
| ||
| B、最大值为1，无最小值 | ||
C、最小值为
| ||
| D、既无最大值也无最小值 |
设随机变量ξ～N（0，1），记Φ（x）=P（ξ＜x），则P（-1＜ξ＜1）等于（ ）
A、
| ||
| B、2Φ（-1）-1 | ||
| C、2Φ（1）-1 | ||
| D、Φ（1）+Φ（-1） |