题目内容
若a＞0，b＞0，则p=
+
与q=a+b的大小关系为（ ）
| b2 |
| a |
| a2 |
| b |
| A、p＞q | B、p≥q |
| C、p＜q | D、p≤q |
考点：不等式比较大小
专题：不等式的解法及应用
分析：根据基本不等式质化简p，问题得以解决．
解答：
解：∵a＞0，b＞0，
∴p=
+
=
≥
•（2ab-ab）=a+b=q．当且仅当a=b时等号成立．
故选：B．
∴p=
| b2 |
| a |
| a2 |
| b |
| (a+b)(a2-ab+b2) |
| ab |
| a+b |
| ab |
故选：B．
点评：本题主要考查了基本不等式，等号成立的条件是关键，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=3x3-ax2+x-5在区间[1，2]上单调递减，则a的取值范围是（ ）
A、[5，
| ||
B、（-∞，5）∪（
| ||
| C、[5，+∞） | ||
D、[
|
已知曲线C1的参数方程为
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0，设曲线C1，C2相交于两点A，B，则过AB中点且与直线AB垂直的直线的直角标方程为（ ）
|
A、y=-
| ||||||||
B、y=
| ||||||||
C、y=-
| ||||||||
D、y=
|
若函数f（x）=x3-
x2+1，则（ ）
| 3 |
| 2 |
A、最大值为1，最小值为
| ||
| B、最大值为1，无最小值 | ||
C、最小值为
| ||
| D、既无最大值也无最小值 |
已知数列{2n-11}，则Sn的最小值为（ ）
| A、S1 |
| B、S5 |
| C、S6 |
| D、S11 |
设随机变量ξ～N（0，1），记Φ（x）=P（ξ＜x），则P（-1＜ξ＜1）等于（ ）
A、
| ||
| B、2Φ（-1）-1 | ||
| C、2Φ（1）-1 | ||
| D、Φ（1）+Φ（-1） |
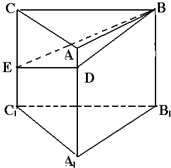如图，已知体积为8，高为4的三棱柱ABC-A1B1C1，CC1⊥平面A1B1C1，点D、E分别在棱AA1和CC1上，且DE⊥B1C1，DA1=3，EC1=2．