题目内容

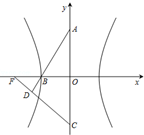如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为3，则∠BDF的余弦值是（　　）
A、
17
51
B、
2
7
51
C、
3
17
51
D、
5
17
51
考点：双曲线的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：利用双曲线的简单性质求出直线方程，求出三角形三个顶点的坐标，利用余弦定理求得cos∠BDF的值．
解答： 解：由题意得A（0，b），C（0，-b），B（-a，0），F（-c，0），
c
a
=3．
∴BF=c-a=2a，BD 的方程为
x
-a
+
y
b
=1，即bx-ay+ab=0，
DC的方程为
x
-c
+
y
b
=1，即bx+cy+bc=0，即bx+3ay+3ab=0，
联立，可得D（-
3a
2
，-
b
2
），又b=2
2
a，
∴FD=
17
2
a，BD=
3a
2
，
△BDF中，由余弦定理得4a2=
17
4
a2+
9
4
a2-2•
17
2
•
3a
2
cos∠BDF，
∴cos∠BDF=
5
17
51
．
故选：D．
点评：本题考查角的余弦值的求法，是中档题，解题时要注意余弦定理和双曲线简单性质的灵活运用．
练习册系列答案
相关题目
由两曲线y=sinx（x∈[0，2π]）和y=cosx（x∈[0，2π]）所围成的封闭图形的面积为
 
．
已知函数f（x）=3x3-ax2+x-5在区间[1，2]上单调递减，则a的取值范围是（　　）
A、[5，
37
4
]
B、（-∞，5）∪（
37
4
，+∞）
C、[5，+∞）
D、[
37
4
，+∞）
在等差数列{an}中，已知ak=1，ak+1=sin2θ，则ak+2=（　　）
A、cos2θ
B、-cos2θ
C、cos2θ
D、-cos2θ
现有语文、数学、英语、物理和化学共5本书，从中任取1本，取出的是理科书的概率为（　　）
A、
1
5
B、
2
5
C、
3
5
D、
4
5
双曲线
x2
5
-
y2
4
=1与
x2
5
-
y2
4
=k始终有相同的（　　）
A、焦点B、准线
C、渐近线D、离心率
已知曲线C1的参数方程为
x=
3
3
t
y=t-
3
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2-2ρcosθ-2ρsinθ+1=0，设曲线C1，C2相交于两点A，B，则过AB中点且与直线AB垂直的直线的直角标方程为（　　）
A、y=-
3
3
x+1+
3
3
B、y=
3
3
x+1+
3
3
C、y=-
3
3
x+1
D、y=
3
3
x+1
若函数f（x）=x3-
3
2
x2+1，则（　　）
A、最大值为1，最小值为
1
2
B、最大值为1，无最小值
C、最小值为
1
2
，无最大值
D、既无最大值也无最小值
已知离心率为
3
2
的椭圆T：
x2
a2
+
y2
b2
=1（a＞0，b＞0）过点M（0，1），过点M引两条互相垂直的直线l1，l2，若P为椭圆上任意一点，记点P到两直线的距离分别为d1，d2，则d12+d22的最大值是（　　）
A、
16
3
B、5
C、
13
4
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网