题目内容
17.已知△ABC中,∠A,∠B,∠C的对边长度分别为a,b,c,已知点O为该三角形的外接圆圆心,点D,E,F分别为边BC,AC,AB的中点,则OD:OE:OF=( )| A. | a:b:c | B. | $\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$ | C. | sinA:sinB:sinC | D. | cosA:cosB:cosC |
分析 根据点O为该三角形的外接圆圆心,半径为R,利用勾股定理求出OD,OE,OF,即可求出OD:OE:OF的值.
解答 解:由题意,点O为该三角形的外接圆圆心,设半径为R,则OA=OB=OC=R,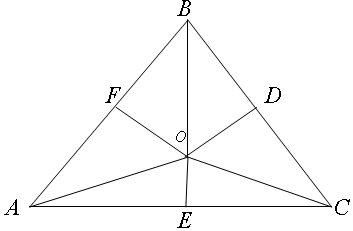
∵D,E,F分别为边BC,AC,AB的中点.
∴OD2=R2-$(\frac{a}{2})^{2}$,OE2=R2-$(\frac{b}{2})^{2}$,OF2=R2-$(\frac{c}{2})^{2}$.
那么OD2:OE2:OF2=($\frac{{a}^{2}}{4si{n}^{2}A}$-$\frac{{a}^{2}}{4}$)2:($\frac{{b}^{2}}{4si{n}^{2}B}$-$\frac{{b}^{2}}{4}$)2:($\frac{{c}^{2}}{4si{n}^{2}C}$-$\frac{{c}^{2}}{4}$)2
开方化简:OD:OE:OF=$\frac{acosA}{sinA}$:$\frac{bcosB}{sinB}$:$\frac{ccosC}{sinC}$
由正弦定理可得:OD:OE:OF=cosA:cosB:cosC.
故选:D.
点评 本题考查了三角形的外接圆的性质和正弦定理的运用.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-2x+2,x≤2\\{log_2}x,x>2\end{array}\right.$,若?x0∈R,使得$f({x_0})≤5m-4{m^2}$成立,则实数m的取值范围为( )
| A. | $[{-1,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},1}]$ | C. | $[{-2,\frac{1}{4}}]$ | D. | $[{\frac{1}{3},1}]$ |
5.已知函数f(x)=aln(x+1)-x2,任意x1,x2∈(0,1),x1>x2时,都有f(x1+1)-f(x2+1)>x1-x2成立,则实数a的取值范围是( )
| A. | a≥15 | B. | a>15 | C. | a<5 | D. | a≤5 |
9.若$P=\sqrt{a+6}+\sqrt{a+7}$,$Q=\sqrt{a+5}+\sqrt{a+8}$,(a>-5),则P,Q的大小关系为( )
| A. | P<Q | B. | P=Q | C. | P>Q | D. | 不能确定 |