题目内容
已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2013)=5,则f(2014)=( )
| A、1 | B、3 | C、5 | D、不能确定 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:将x=2013代入解析式表示出f(2013),代入f(2013)=5值计算得到asinα+bcosβ的值,再将x=2014代入即可求出f(2014)的值.
解答:
解:当x=2013时,f(2013)=asin(2013π+α)+bcos(2013π+β)+4=-asinα-bcosβ+4=5,即asinα+bcosβ=-1,
当x=2014时,f(2014)=asin(2014π+α)+bcos(2014π+β)+4=asinα+bcosβ+4=-1+4=3.
故选:B.
当x=2014时,f(2014)=asin(2014π+α)+bcos(2014π+β)+4=asinα+bcosβ+4=-1+4=3.
故选:B.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于函数f(x),若存在区间M=[a,b],(a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间”,现有四个函数:
①f(x)=x2;
②f(x)=sin(
x);
③f(x)=lnx
④f(x)=x3-3x
其中存在“稳定区间”的函数为( )
①f(x)=x2;
②f(x)=sin(
| π |
| 2 |
③f(x)=lnx
④f(x)=x3-3x
其中存在“稳定区间”的函数为( )
| A、① | B、①② | C、①②③ | D、①②④ |
直线xcosθ+ysinθ-2=0与圆(x-sinθ)2+(y-2cosθ)2=
(θ∈R)的位置关系为( )
| 1 |
| 4 |
| A、相交,相切或相离 |
| B、相切 |
| C、相切或相离 |
| D、相交或相切 |
一个长方体被一平面截去一部分所得几何体的三视图如图,则该几何体的体积是( )


| A、1440 | B、1200 |
| C、960 | D、720 |
已知α,β是任意角,则“sinα=cosα”是“cos(α+β)=sin(α-β)”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
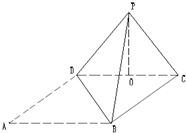 矩形ABCD中,AB=6,BC=2
矩形ABCD中,AB=6,BC=2