题目内容
已知点O是锐角△ABC的外心，AB=8，AC=12，A=
．若
=x
+y
，则6x+9y= ．
| π |
| 3 |
| AO |
| AB |
| AC |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图，O点在AB，AC上的射影是点D，E，它们分别为AB，AC的中点，由数量积的几何意义，即可得出．
解答：
解：如图，O点在AB，AC上的射影是点D，E，则它们分别为AB，AC的中点，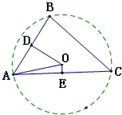
•
=|
|•|
|=32，
•
=|
|•|
|=72，
依题意有：
•
=x
2+y
•
=64x+48y=32，即4x+3y=2，
•
=x
•
+y
2=48x+144y=72，即2x+6y=3，
将两式相加可得：6x+9y=5．
故答案为：5．
| AB |
| AO |
| AB |
| AD |
| AC |
| AO |
| AC |
| AE |
依题意有：
| AB |
| AO |
| AB |
| AC |
| AB |
| AC |
| AO |
| AB |
| AC |
| AC |
将两式相加可得：6x+9y=5．
故答案为：5．
点评：本题考查了向量的投影、垂经定理、数量积运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
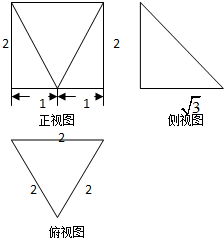一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）| A、9π | ||
B、
| ||
| C、8π | ||
| D、7π |
已知在△ABC中，D是AB边上的一点，
=λ（
+
），|
|=2，|
|=1，若
=
，
=
，则用
，
表示
为（ ）
| CD |
| ||
|
|
| ||
|
|
| CA |
| CB |
| CA |
| b |
| CB |
| a |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
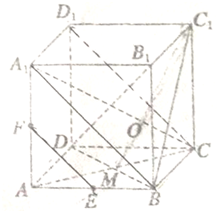如图，在正方体ABCD-A1B1C1D1，对角线A1C与平面BDC1交于点O．AC、BD交于点M、E为AB的中点，F为AA1的中点，