题目内容
设x，y满足x+y=40且x，y都是正数，则xy的最大值是（ ）
| A、400 | B、100 |
| C、40 | D、20 |
考点：基本不等式
专题：函数的性质及应用
分析：由条件利用基本不等式求得xy的最大值．
解答：
解：由于x、y都是正数，且x+y=40，利用基本不等式可得 40≥2
，即 xy≤400，
当且仅当x=y=20时，等号成立，
故选：A．
| xy |
当且仅当x=y=20时，等号成立，
故选：A．
点评：本题主要考查基本不等式的应用，注意基本不等式的使用条件，以及等号成立的条件，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
一个建筑队承包了两项工程，每项工程均有三项任务，由于工序的要求，第一项工程必须按照任务A、任务B、任务C的先后顺序进行，第二项工程必须按照任务D、任务E、任务F的先后顺序进行，建筑队每次只能完成一项任务，但第一项工程和第二项工程可以自由交替进行，若公司将两项工程做完，共有多少种安排方法（ ）
| A、12 | B、30 | C、20 | D、48 |
当x=a时，函数y=ln（x+2）-x取到极大值b，则ab等于（ ）
| A、-1 | B、0 | C、1 | D、2 |
函数f（x）的导函数f′（x）的图象如图所示，则（ ）
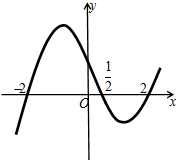
A、x=
| ||
| B、x=-2为f（x）的极大值点 | ||
| C、x=2为f（x）的极大值点 | ||
| D、x=0为f（x）的极小值点 |
如图，将等差数列{an}的前6项填入一个三角形的顶点及各边中点的位置，且在图中每个三角形顶点所填的三项也成等差数列，数列{an}的前2012项和S2012=4024，则满足nan＞an的n的值为（ ）| A、2012 | B、4024 |
| C、2 | D、3 |
如果生男孩和生女孩的概率相等，有一对夫妻生有3个小孩，已知这对夫妻的孩子有一个是女孩，那么这对夫妻有男孩的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=x3+ax2+bx+a2在x=1时有极值10，则a的值为（ ）
| A、-3或4 | B、4 |
| C、-3 | D、3或4 |
过点P（0，1）与圆（x-1）2+y2=4相交的所有直线中，被圆截得的弦最长的直线方程是（ ）
| A、x+y-1=0 |
| B、x-y+1=0 |
| C、x=0 |
| D、y=1 |