Question

函数f（x）的导函数f′（x）的图象如图所示，则（　　）

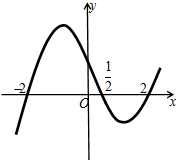
• A、x=

  1

  2

  为f（x）的极大值点
• B、x=-2为f（x）的极大值点
• C、x=2为f（x）的极大值点
• D、x=0为f（x）的极小值点

Answer 1

考点：利用导数研究函数的极值

专题：导数的概念及应用

分析：根据图象找到函数的单调区间，画出函数的草图，从而找到函数的极大值点．

解答： 解：由图象得；
函数f（x）在（-∞，-2）递减，在（-2，

1

2

）递增，
在（

1

2

，2）递减，在（2，+∞）递增，
画出函数的草图得：
，
由图象得；x=

1

2

是函数f（x）的极大值点，
故选；A．

点评：本题考察了函数的单调性，函数的极值问题，导数的应用，是一道基础题．