题目内容
当x∈(0,
)时,求函数f(x)=
的值域.
| π |
| 6 |
| cosx |
| 1-sinx |
考点:三角函数的最值
专题:三角函数的求值
分析:本题给出的表达式
,恰好符合已知两点(x1,y1),(x2,y2)求斜率的公式:k=
,利用数形结合的方法求出斜率范围即可.
| cosx |
| 1-sinx |
| y2-y1 |
| x2-x1 |
解答:
 解:
解:
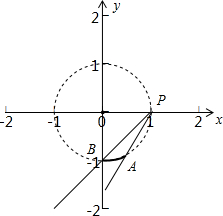
可看作求点(1,0)与(sinx,-cosx)连线的斜率,
x∈(0,
),sinx∈(0,
),-cosx∈(-1,-
).
(sinx,-cosx)表示圆x2+y2=1上的一段弧.kPA=
=
,kPB=
=1.
函数f(x)=
的值域(1,
),
 解:
解:| cosx |
| 1-sinx |
x∈(0,
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
(sinx,-cosx)表示圆x2+y2=1上的一段弧.kPA=
-
| ||||
|
| 3 |
| -1-0 |
| 0-1 |
函数f(x)=
| cosx |
| 1-sinx |
| 3 |
点评:若已知A(x1,y1),B(x2,y2),则AB所在直线的斜率 k=
,数形结合思想有时候解决问题很有效.注意斜率的求法.
| y2-y1 |
| x2-x1 |

练习册系列答案
相关题目
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=3-x2 | ||
B、y=
| ||
| C、y=log2|x| | ||
| D、y=x3+1 |
设a∈Z,且0≤a<13,若512014+a能被13整除,则a=( )
| A、11 | B、12 | C、1 | D、3 |
等差数列{an}中,a1=1,a2=3,数列{
}的前n项和为
,则n的值为( )
| 1 |
| anan+1 |
| 15 |
| 31 |
| A、15 | B、16 | C、17 | D、18 |
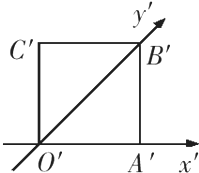 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )
一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )