题目内容
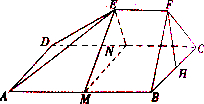 如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.
如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.(1)若M、N分别是AB、CD的中点,求证:平面MNE∥平面BCF;
(2)若△BCF中,BC边上的高FH=3,求多面体的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)由ABCD是正方形,M、N是AB、CD中点,得MN∥BC,从而BFEM是平行四边形,由此能证明平面MNE∥平面BCF.
(2)分别求出四棱锥E-AMND的体积和三棱柱MNE-BCF的体积,由此能求出多面体EF-ABCD的体积.
(2)分别求出四棱锥E-AMND的体积和三棱柱MNE-BCF的体积,由此能求出多面体EF-ABCD的体积.
解答:
(1)证明:∵ABCD是正方形,M、N是AB、CD中点,
∴MN∥BC,
∵MB=2=EF,EF∥AB,
∴BFEM是平行四边形,
∴ME∥BF,
∵MN,ME?平面MNE,BC,BF?平面BCF,
∴平面MNE∥平面BCF
(2)解:∵EF∥AB,
∴四棱锥E-AMND的高就是FH,
∴四棱锥E-AMND的体积V1=
×2×4×3=8,
∵平面FBC⊥平面ABCD,
∴MB就是三棱柱MNE-BCF的高,
∴三棱柱MNE-BCF的体积V2=4×3÷2×2=12,
∴多面体EF-ABCD的体积V=V1+V2=20.
∴MN∥BC,
∵MB=2=EF,EF∥AB,
∴BFEM是平行四边形,
∴ME∥BF,
∵MN,ME?平面MNE,BC,BF?平面BCF,
∴平面MNE∥平面BCF
(2)解:∵EF∥AB,
∴四棱锥E-AMND的高就是FH,
∴四棱锥E-AMND的体积V1=
| 1 |
| 3 |
∵平面FBC⊥平面ABCD,
∴MB就是三棱柱MNE-BCF的高,
∴三棱柱MNE-BCF的体积V2=4×3÷2×2=12,
∴多面体EF-ABCD的体积V=V1+V2=20.
点评:本题考查平面与平面平行的证明,考查几何体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
设a∈Z,且0≤a<13,若512014+a能被13整除,则a=( )
| A、11 | B、12 | C、1 | D、3 |
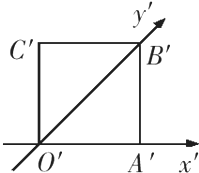 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )
一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )