Question

如图，已知正三角形BCD外一点A满足AB=AC=AD．E、F分别是AB、BC的中点，且EF⊥DE，则∠BAC=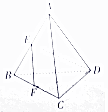

 

．

Answer 1

考点：棱锥的结构特征

专题：解三角形,空间角

分析：根据题意，设AB=AC=AD=x，BC=CD=BD=a，DE=y，
利用余弦定理，在△BDE中，得出BD²=BE²+DE²-2BE•DEcos∠BED①，
在△ADE中，得出AD²=AE²+DE²-2AE•DEcos∠AED②，
由①、②，结合△DEF中，EF⊥DE，可以求出BC²=AB²+AC²，得出△BAC是等腰直角三角形，求出∠BAC的值．

解答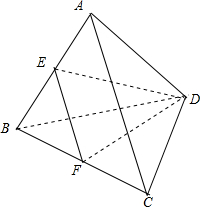： 解：如图所示，
设AB=AC=AD=x，BC=CD=BD=a，DE=y，
则EF=

x

2

，DF=

3

2

a，
在△BDE中，由余弦定理得，
BD²=BE²+DE²-2BE•DEcos∠BED，
即a²=(

x

2

)2+y²-2•

x

2

•y•cos∠BED①，
在△ADE中，由余弦定理得，
AD²=AE²+DE²-2AE•DEcos∠AED，
即x²=(

x

2

)2+y²-2•

x

2

•y•cos（π-∠BED）②，
①+②得，a²+x²=

x2

2

+2y²，
∴y²=

a2

2

+

x2

4

；
在△DEF中，∵EF⊥DE，∴DF²=EF²+DE²，
即(

3

2

a)2=(

x

2

)2+y²=(

x

2

)2+

a2

2

+

x2

4

∴a²=2x²，
即BC²=AB²+AC²，
∴△BAC是等腰直角三角形，∴∠BAC=90°．
故答案为：90°．

点评：本题考查了余弦定理的应用问题，也考查了勾股定理的应用问题，考查了方程思想的应用问题，是中档题目．