题目内容
一条直线过点P(-3,-
),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为 .
| 3 |
| 2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:分类讨论,利用点到直线的距离公式,即可得出结论.
解答:
解:当直线的斜率不存在时,直线方程为x=-3,圆x2+y2=25的圆心(0,0)到该直线的距离为3,满足题意;
当直线的斜率存在时,设直线斜率为k,
则方程为y+
=k(x+3),
即2kx-2y+6k-3=0,圆x2+y2=25的圆心到该直线的距离为
=3,∴k=-
,
∴直线的方程为3x+4y+15=0
∴所求直线的方程为x=-3或3x+4y+15=0.
故答案为:x=-3或3x+4y+15=0
当直线的斜率存在时,设直线斜率为k,
则方程为y+
| 3 |
| 2 |
即2kx-2y+6k-3=0,圆x2+y2=25的圆心到该直线的距离为
| |6k-3| | ||
|
| 3 |
| 4 |
∴直线的方程为3x+4y+15=0
∴所求直线的方程为x=-3或3x+4y+15=0.
故答案为:x=-3或3x+4y+15=0
点评:本题考查直线方程,考查分类讨论的数学思想,考查点到直线的距离公式的运用,属于中档题.

练习册系列答案
相关题目
下列各函数中,为指数函数的是( )
| A、y=(-1.3)x | ||
B、y=(
| ||
C、y=x
| ||
| D、y=2x2 |
把正方形ABCD沿对角线BD折成直二角后,下列命题正确的是( )
| A、AB⊥BC |
| B、AC⊥BD |
| C、CD⊥平面ABC |
| D、平面ABC⊥平面ACD |
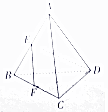
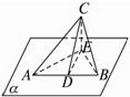 Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.
Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.