题目内容
已知点M是抛物线y2=x上一动点,以OM为一边(O为原点)作正方形MNPO,求动点P的轨迹方程.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意画出图形,设出抛物线上任一点M(m2,m),(m为任意实数),求得P点的坐标相应为(m,-m2),即得到P的横纵坐标所满足的函数关系,同理得到MNPO逆时针时的P的轨迹方程.
解答:
解:如图,
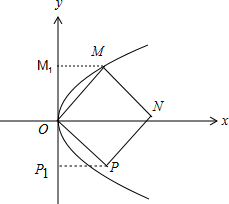 作PP1、MM1垂直于y轴,则三角形OPP1、OMM1全等,
作PP1、MM1垂直于y轴,则三角形OPP1、OMM1全等,
∴对任一点M(m2,m),(m为任意实数),
P点的坐标相应为(m,-m2),
故P点横、纵坐标满足关系 y=-x2,
这就是动点P的轨迹方程;
当所求正方形与上图关于OM对称时,
此时动点P的轨迹方程为 y=x2.
 作PP1、MM1垂直于y轴,则三角形OPP1、OMM1全等,
作PP1、MM1垂直于y轴,则三角形OPP1、OMM1全等,∴对任一点M(m2,m),(m为任意实数),
P点的坐标相应为(m,-m2),
故P点横、纵坐标满足关系 y=-x2,
这就是动点P的轨迹方程;
当所求正方形与上图关于OM对称时,
此时动点P的轨迹方程为 y=x2.
点评:本题考查了抛物线的简单几何性质,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
方程|x|-1=1-(y-1)2 所表示的曲线是( )
| A、一个圆 | B、两个圆 |
| C、两条抛物线 | D、两个半圆 |
下列各函数中,为指数函数的是( )
| A、y=(-1.3)x | ||
B、y=(
| ||
C、y=x
| ||
| D、y=2x2 |