题目内容
10.已知f(x)=(x2-2ax)lnx+2ax-$\frac{1}{2}$x2,其中a∈R.(1)若a=0,且曲线f(x)在x=t处的切线l过原点,求直线l的方程;
(2)求f(x)的极值;
(3)若函数f(x)有两个极值点x1,x2(x1<x2),证明f(x1)+f(x2)<$\frac{1}{2}$a2+3a.
分析 (1)求出导函数,根据切线的和导函数的关系求解 即可;、
(2)求出导函数f'(x)=(2x-2a)lnx,对a进行分类讨论,在不同区间求出函数的单调性,进而判断函数的最值问题;
(3)根据(2)可知a的范围,得出f(x1)+f(x2)=f(a)+f(1),作差放缩可得$f({x_1})+f({x_2})-(\frac{1}{2}{a^2}+3a)$=$-{a^2}lna+{a^2}-a-\frac{1}{2}<-{a^2}(lna-1+\frac{1}{a})$,构造函数$g(a)=lna-1+\frac{1}{a}$,利用导函数得出函数的单调性,得出g(a)>g(1)=0,得出结论.
解答 解:(1)当a=0时,$f(x)={x^2}lnx-\frac{1}{2}{x^2}$,f'(x)=2xlnx,所以切线I的斜率k=f'(t)=2tlnt,又直线I过原点,所以k=tlnt-$\frac{1}{2}$t,
,由2tlnt=tlnt-$\frac{1}{2}$t,得lnt=-$\frac{1}{2}$,t=$\frac{1}{\sqrt{e}}$.所以k=f'(-$\frac{1}{\sqrt{e}}$)=-$\frac{1}{\sqrt{e}}$,故切线I的方程为y=-$\frac{x}{\sqrt{e}}$.
(2)由f(x)=(x2-2ax)lnx+2ax-$\frac{1}{2}$x2,可得f'(x)=(2x-2a)lnx,
①当a≤0时f'(x)>0得x>1,f'(x)<0得0<x<1,
f(x)在(1,+∞)上单调递增,在(0,1)上单调递减,f(x)在x=1时取到极小值,且f(1)=2a-$\frac{1}{2}$,f(x)没有极大值.
②当0<a<1时,f'(x)>0得x>1或0<x<a,f'(x)<0得a<x<1.f(x)在(0,a),(1,+∞)上单调递增,在(a,1)上单调递减,
f(x)在x=a时取到极大值,且f(a)=-a2lna+$\frac{3}{2}{a}^{2}$,f(x)在x=1时取到极小值,且f(1)=2a-$\frac{1}{2}$;
③当a=1时f'(x)≥0恒成立恒成立,f(x)在R上单调递增,f(x)没有极大值也没有极小值;
④当a>1时f'(x)>0得x>a或0<x<1,f'(x)<0得1<x<a,f(x)在(0,1),(a,+∞)上单调递增,在(1,a)上单调递减,f(x)在x=a时取到极小值,且f(a)=-a2lna+$\frac{3}{2}{a}^{2}$,.f(x)在x=1时取到极大值,且f(1)=2a-$\frac{1}{2}$;
综上可得,当a≤0时,f(x)在x=1时取到极小值2a-$\frac{1}{2}$,f(x)没有极大值;
当0<a<1时,f(x)在x=a时取到极大值-a2lna+$\frac{3}{2}{a}^{2}$,在x=1时取到极小值2a-$\frac{1}{2}$;
当a=1时,f(x)没有极大值也没有极小值;
当a>1时,f(x)在x=a时取到极小值$-{a^2}lna+\frac{3}{2}{a^2}$,在x=1时取到极大值$2a-\frac{1}{2}$.
(3)由(2)知当a>0且a≠1时,f(x)有两个极值f(x)点x1,x2,且f(x1)+f(x2)=f(a)+f(1),$f({x_1})+f({x_2})-(\frac{1}{2}{a^2}+3a)$=$-{a^2}lna+{a^2}-a-\frac{1}{2}<-{a^2}(lna-1+\frac{1}{a})$,
设$g(a)=lna-1+\frac{1}{a}$,则$g'(a)=\frac{1}{a}-\frac{1}{a^2}=\frac{a-1}{a^2}$,所以g(a)在(0,1)上单调递减,在(1,+∞)上单调递增,由a>0且a≠1可得g(a)>g(1)=0,所以$f({x_1})+f({x_2})-(\frac{1}{2}{a^2}+3a)<$$-{a^2}(lna-1+\frac{1}{a})<0$,即$f({x_1})+f({x_2})<\frac{1}{2}{a^2}+3a$.
点评 本题考查了导函数的综合应用和参数的分类讨论,难点是参数的讨论和函数的构造.

| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
 下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:
下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y对x的回归直线方程;
(3)已知该公司技术升级前生产100吨A产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨A产品的成本比技术升级前约降低多少万元?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{1}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)
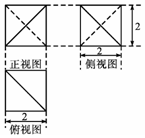 如图是某多面体的三视图,则该几何体的外接球体积为4$\sqrt{3}$π.
如图是某多面体的三视图,则该几何体的外接球体积为4$\sqrt{3}$π.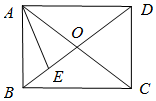 在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.
在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.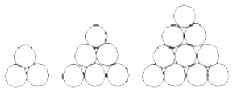 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).