题目内容
3.若函数f(x)为奇函数,且在(0,+∞)上是增函数,又f(-3)=0,则不等式x[f(-x)-f(x)]<0的解集为( )| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
分析 根据题意,由函数f(x)为奇函数分析可得x[f(-x)-f(x)]<0?xf(x)>0,结合函数的单调性以及f(-3)=0分2种情况讨论:①、当x∈(-∞,-3)∪(0,3)上②、当x∈(-3,0)∪(3,+∞)上,分别求出每种情况下x的取值范围,综合即可得答案.
解答 解:若函数f(x)为奇函数,则f(-x)=-f(x),
则x[f(-x)-f(x)]<0⇒x[-2f(x)]<0⇒xf(x)>0,
若奇函数f(x)在(0,+∞)上为增函数,则函数f(x)在(-∞,0)上也为增函数,
又由f(-3)=0,则f(3)=0;
分2种情况讨论:
①、当x∈(-∞,-3)∪(0,3)上时,f(x)<0,
若xf(x)>0,必有x<0,
此时x[f(-x)-f(x)]<0的解集为(-∞,-3),
②、当x∈(-3,0)∪(3,+∞)上时,f(x)>0,
若xf(x)>0,必有x>0,
此时x[f(-x)-f(x)]<0的解集为(3,+∞),
综合可得:不等式x[(f(x)-f(-x)]<0的解集为(-∞,-3)∪(3,+∞);
故选:D.
点评 本题考查函数的奇偶性与单调性的综合应用,其中奇函数在对称区间上单调性相同,是解答本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
14.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
8.已知f′(x)为函数f(x)的导函数,且$f(x)=\frac{1}{2}{x^2}-f(0)+f'(1){e^{x-1}}$,若$g(x)=f(x)-\frac{1}{2}{x^2}+x$,则方程$g(\frac{x^2}{a}-x)-x=0$有且仅有一个根时,a的取值范围是( )
| A. | [1,+∞) | B. | (-∞,1] | C. | (0,1] | D. | (-∞,0)∪{1} |
15.过抛物线C:y2=2px(p>0)的焦点F作斜率为$\frac{4}{3}$的直线l与C及其准线分别相交于A、B、D三点,则$\frac{|AD|}{|BD|}$的值为( )
| A. | 2或$\frac{1}{2}$ | B. | 3或$\frac{1}{3}$ | C. | 1 | D. | 4或$\frac{1}{4}$ |
12.已知f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则f'(0)=( )
| A. | n | B. | n-1 | C. | $\frac{n(n-1)}{2}$ | D. | $\frac{1}{2}$n(n+1) |
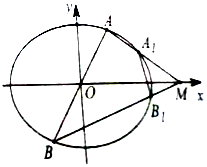 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1