题目内容
1.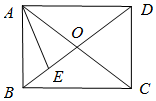 在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.
在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.
分析 由向量的线性运算得$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AO}$=$\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AD}$.即可.
解答 解:$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AO}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AD})$
=$\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AD}$.
∴$λ=\frac{3}{4},μ=\frac{1}{4}$,∴$λμ=\frac{3}{16}$
故答案为:$\frac{3}{16}$
点评 本题考查了平面向量的线性运算,转化思想,数形结合思想,属于基础题.

练习册系列答案
相关题目
12.第17届亚运会于2014年9月19日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?参考公式:K2=$\frac{n(ad-b{c)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
(1)根据以上数据完成以下2×2列联表:
| 喜爱运 动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?参考公式:K2=$\frac{n(ad-b{c)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
15.过抛物线C:y2=2px(p>0)的焦点F作斜率为$\frac{4}{3}$的直线l与C及其准线分别相交于A、B、D三点,则$\frac{|AD|}{|BD|}$的值为( )
| A. | 2或$\frac{1}{2}$ | B. | 3或$\frac{1}{3}$ | C. | 1 | D. | 4或$\frac{1}{4}$ |
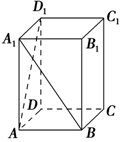 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.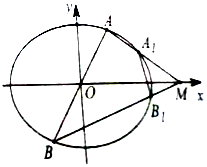 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1 某几何体的三视图如图所示(单位:cm),则该几何体的体积V=6cm3,表面积S=16+2$\sqrt{5}$cm2.
某几何体的三视图如图所示(单位:cm),则该几何体的体积V=6cm3,表面积S=16+2$\sqrt{5}$cm2.