题目内容
15.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{3}}{2}$),离心率为$\frac{\sqrt{3}}{2}$,点A为椭圆C的右顶点,直线l与椭圆相交于不同于点A的两个点P(x1,y1),Q(x2,y2).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)当$\overrightarrow{AP}$⊥$\overrightarrow{AQ}$=0时,求△OPQ面积的最大值.
分析 (Ⅰ)将点代入椭圆方程,根据椭圆的离心率公式,即可求得a和b的值,即可求得椭圆方程;
(Ⅱ)分类讨论.当直线l的斜率不存在时,求得P,Q点坐标,由$\overrightarrow{AP}$⊥$\overrightarrow{AQ}$=0即可求得m的值,求得丨PQ丨,即可求得△OPQ面积;
当直线l的斜率存在,且不为0,代入椭圆方程,利用韦达定理,弦长公式及向量数量积的坐标运算,根据函数的单调性即可求得△OPQ面积的最大值.
解答 解:(Ⅰ)由题意知:且$\left\{{\begin{array}{l}{\frac{c}{a}=\frac{{\sqrt{3}}}{2}}\\{{a^2}={b^2}+{c^2}}\\{\frac{1}{a^2}+\frac{3}{{4{b^2}}}=1}\end{array}}\right.$,可得:$\left\{{\begin{array}{l}{a=2}\\{b=1}\\{c=\sqrt{3}}\end{array}}\right.$,
椭圆C的标准方程为$\frac{x^2}{4}+{y^2}=1$…(4分)
(Ⅱ)当直线l的斜率不存在时,设l:x=m,与$\frac{x^2}{4}+{y^2}=1$,联立得$P(m,\sqrt{1-\frac{m^2}{4}}),Q(m,-\sqrt{1-\frac{m^2}{4}})$.
由于$\overrightarrow{AP}•\overrightarrow{AQ}=0$,得${({m-2})^2}-({1-\frac{m^2}{4}})=0$,解得$m=\frac{6}{5}$或m=2(舍去).
此时$|{PQ}|=\frac{8}{5}$,△OPQ的面积为$\frac{24}{25}$…(6分)
当直线l的斜率存在时,由题知k≠0,设l:y=kx+m,与$\frac{x^2}{4}+{y^2}=1$联立,
整理得:(4k2+1)x2+8kmx+4(m2-1)=0.由△>0,得4k2-m2+1>0;
且${x_1}+{x_2}=\frac{-8km}{{4{k^2}+1}}$,${x_1}{x_2}=\frac{{4({{m^2}-1})}}{{4{k^2}+1}}(*)$…(7分)
由于$\overrightarrow{AP}•\overrightarrow{AQ}=0$,得:$({x_1}-2)({x_2}-2)+{y_1}{y_2}=({k^2}+1){x_1}{x_2}+({km-2})({{x_1}+{x_2}})+({{m^2}+4})=0$.
代入(*)式得:12k2+5m2+16km=0,即$m=-\frac{6}{5}k$或m=-2k(此时直线l过点A,舍去).
$|{PQ}|=\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\frac{4}{{4{k^2}+1}}\sqrt{({1+{k^2}})({4{k^2}-{m^2}+1})}$,
点O到直线l的距离为:$d=\frac{|m|}{{\sqrt{{k^2}+1}}}$…(10分)
S△OPQ=$\frac{{2|m|\sqrt{4{k^2}-{m^2}+1}}}{{4{k^2}+1}}$,将$m=-\frac{6}{5}k$代入得:${S_{△OPQ}}=\frac{12}{25}•\sqrt{\frac{{64{k^4}+25{k^2}}}{{{{(4{k^2}+1)}^2}}}}$,
令$4{k^2}+1=\frac{1}{p}$0<p<1,${S_{△OPQ}}=\frac{6}{25}•\sqrt{-9{p^2}-7p+16}$,由y=-9p2-7p+16,
在(0,1)上递减,
∴0<y<16,故${S_{△OPQ}}∈(0,\;\;\frac{24}{25})$,
综上(S△OPQ)max=$\frac{24}{25}$…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式及向量数量积的坐标运算,函数单调性与椭圆的应用,考查计算能力,属于中档题.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案| A. | x2+y2=16 | B. | x2+y2=16(x≥4) | C. | x2-y2=16 | D. | x2-y2=16(x≥4) |
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
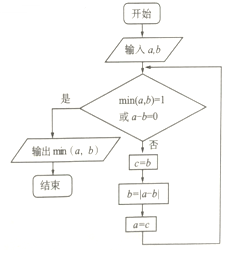 min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )
min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )