题目内容
8.下列函数中,既不是奇函数,也不是偶函数的是( )| A. | $y={2^x}+\frac{1}{2^x}$ | B. | $y=sinx+\frac{1}{x}$ | C. | y=x2+cosx | D. | $y=x+\frac{1}{x^2}$ |
分析 对选项弦求出定义域,再计算f(-x),与f(x)比较,由奇偶性的定义,即可判断.
解答 解:对A,函数定义域为R,f(-x)=2-x+$\frac{1}{{2}^{-x}}$=2x+$\frac{1}{{2}^{x}}$=f(x),即为偶函数;
对B,函数定义域为{x|x≠0},f(-x)=sin(-x)-$\frac{1}{x}$=-(sinx+$\frac{1}{x}$)=-f(x),即为奇函数;
对C,y=x2+cosx的定义域为R,f(-x)=cos(-x)+(-x)2=cosx+x2=f(x),即为偶函数;
对D,函数定义域为{x|x≠0},f(-x)=-x+$\frac{1}{{x}^{2}}$≠f(x),且≠-f(x),即为非奇非偶函数.
故选:D.
点评 本题考查函数的奇偶性的判断,注意运用定义法,考查运算能力,属于基础题.

练习册系列答案
相关题目
17.已知命题p:“?x0∈R,x03>x0”,则命题¬p为( )
| A. | ?x∈R,x3>x | B. | ?x∈R,x3<x | C. | ?x∈R,x3≤x | D. | ?x0∈R,x03≤x0 |
18.函数$y=tan(2x-\frac{π}{3})$的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
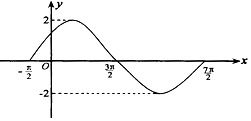 已知f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)在一个周期内图象如图所示.
已知f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)在一个周期内图象如图所示.