Question

20．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的右焦点F作圆x²+y²=a²的切线FM，交y轴于点P，切圆于点M，若$2\overrightarrow{OM}=\overrightarrow{OF}+\overrightarrow{OP}$，则双曲线的离心率是$\sqrt{2}$．

Answer 1

分析 根据向量加法法则，得到OM是△POF中PF边上的中线．由PF与圆x²+y²=a²相切得到OM⊥PF，从而可得△POF是等腰直角三角形，∠MFO=45°．最后在Rt△OMF利用三角函数的定义算出$\frac{a}{c}$=$\frac{\sqrt{2}}{2}$，可得双曲线的离心率大小．

解答 解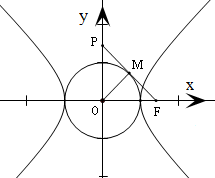：∵$2\overrightarrow{OM}=\overrightarrow{OF}+\overrightarrow{OP}$，
∴△POF中，OM是PF边上的中线．
∵PF与圆x²+y²=a²相切，∴OM⊥PF，
由此可得△POF中，PO=FO，∠MFO=45°，
又∵Rt△OMF中，OM=a，OF=c，
∴sin∠MFO=$\frac{\sqrt{2}}{2}$，即$\frac{a}{c}$=$\frac{\sqrt{2}}{2}$．
因此，双曲线的离心率e=$\sqrt{2}$．
故答案为$\sqrt{2}$．

点评 本题在双曲线中给出向量关系式，在直线与圆相切的情况下求双曲线的离心率．着重考查了解直角三角形、向量的加法法则、直线与圆的位置关系和双曲线的简单性质等知识，属于中档题．