题目内容

已知△ABC中，a、b、c分别为∠A、∠B、∠C的三条对边，a=5，b=3，∠C=120°，则sinA的值为
 
．
考点：余弦定理,正弦定理
专题：解三角形
分析：利用余弦定理求出c，再用正弦定理求sinA．
解答： 解：∵△ABC中，a、b、c分别为∠A、∠B、∠C的三条对边，
a=5，b=3，∠C=120°，
∴c=
25+9-2×5×3×cos120°
=7，
∴
7
sin120°
=
5
sinA
，
∴sinA=
5sin120°
7
=
5
3
14
．
故答案为：
5
3
14
．
点评：本题考查角的正弦值的求法，是基础题，解题时要认真审题，注意余弦定理和正弦定理的合理运用．
练习册系列答案
相关题目
对于函数y=f（x），“y=f（x）是奇函数”是“y=|f（x）|的图象关于y轴对称”的
 
条件．（填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”之一）
设集合A={1，2，3}，集合B={x|x2-1=0}．
（1）求A∩B；
（2）若全集U={1，2，3，4，-1}，求∁U（A∪B）．
已知集合A={x|x-4≤0}，B={x|-3≤x≤m}，且A∪B=A，则m的取值范围
 
．
已知集合A的元素全为实数，且满足：若a∈A，则
1+a
1-a
∈A．若a=-3，请写出集合A中所有元素
 
．
定义“[x]”，其中[x]表示不超过x的最大整数，记函数f（x）=[x[x]]，x∈R．
（1）若集合A={x|[x]2-2[x]-3≤0}，B={x||f（x）-1|≤1}，求集合A，B；
（2）当x∈[0，2n），n∈N*时，记函数f（x）的值域中的元素个数为an，求证：
1
a1-1
+
1
a2-1
+…+
1
an-1
＜
11
9
，n∈N*．
已知A、B、C是△ABC的三个内角，a、b、c为其对应边，向量
m
=（-1，
3
），
n
=（cosA，sinA），且
m
•
n
=1
（1）求角A；
（2）若c=
5
，
cosB
cosC
=
b
c
，求△ABC的面积S．
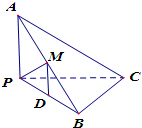如图，已知三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．
（1）求证：DM∥平面APC；
（2）求证：BC⊥平面APC．
已知函数f（x）=x2-4ax+2a+6（x∈R）．
（1）求函数的最小值为0时的a的值；
（2）若函数f（x）的值均为非负值，求函数g（a）=2-a|a+3|的值域；
（3）若对任意x1，x2∈[0，2]，都有|f（x1）-f（x2）|≤1成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网