题目内容
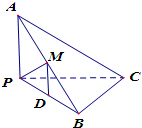如图，已知三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．（1）求证：DM∥平面APC；
（2）求证：BC⊥平面APC．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）要证明线面平行，可以通过线线平行来转化，然后利用中位线定理，进一步利用线面平行的判定定理进行证明．
（2）要证线面垂直，可以通过线线垂直和线面垂直来转化，最后利用线面垂直的判定证明结论．
（2）要证线面垂直，可以通过线线垂直和线面垂直来转化，最后利用线面垂直的判定证明结论．
解答：
证明：（1）已知三棱锥A-BPC中
∵M为AB中点，D为PB中点
∴DM∥AP
AP?平面APC，DM?平面APC
∴DM∥平面APC
（2）△PMB为正三角形，D为PB中点
∴DM⊥PB
在平面APB中，DM∥AP
∴AP⊥PB
∵AP⊥PC
∴AP⊥平面PBC
∴AP⊥BC
∵AC⊥BC
∴BC⊥平面APC
证明：（1）已知三棱锥A-BPC中
∵M为AB中点，D为PB中点
∴DM∥AP
AP?平面APC，DM?平面APC
∴DM∥平面APC
（2）△PMB为正三角形，D为PB中点
∴DM⊥PB
在平面APB中，DM∥AP
∴AP⊥PB
∵AP⊥PC
∴AP⊥平面PBC
∴AP⊥BC
∵AC⊥BC
∴BC⊥平面APC
点评：本题考查的知识点：线面平行的判定定理，线面垂直的性质定理和判定定理之间的相互转换．
练习册系列答案
相关题目
已知sin（α-2π）=2sin（
π+α），且α≠kπ+
（k∈Z），则
的值为（ ）
| 3 |
| 2 |
| π |
| 2 |
| 3sin2α-sin2α |
| 3+cos2α |
A、
| ||
B、
| ||
C、
| ||
D、
|
命题：?x，y∈R，如果xy=0，则x=0．它的否命题为（ ）
| A、?x，y∈R，如果xy≠0，则x≠0 |
| B、?x，y∈R，如果xy=0，则x≠0 |
| C、?x，y∈R，如果xy≠0，则x≠0 |
| D、?x，y∈R，如果xy=0，则x≠0 |
如图，已知正三角形PAD，正方形ABCD，平面PAD⊥平面ABCD，E为PD的中点．