题目内容
设集合A={1，2，3}，集合B={x|x2-1=0}．
（1）求A∩B；
（2）若全集U={1，2，3，4，-1}，求∁U（A∪B）．
（1）求A∩B；
（2）若全集U={1，2，3，4，-1}，求∁U（A∪B）．
考点：交、并、补集的混合运算,交集及其运算
专题：集合
分析：（1）求出B中方程的解确定出B，求出A与B的交集即可；
（2）求出A与B的并集，找出并集的补集即可．
（2）求出A与B的并集，找出并集的补集即可．
解答：
解：（1）由B中方程解得：x=1或x=-1，即B={-1，1}，
∵A={1，2，3}，
∴A∩B={1}；
（2）∵A={1，2，3}，B={-1，1}，
∴A∪B={-1，1，2，3}，
∵U={1，2，3，4，-1}，
∴∁U（A∪B）={4}．
∵A={1，2，3}，
∴A∩B={1}；
（2）∵A={1，2，3}，B={-1，1}，
∴A∪B={-1，1，2，3}，
∵U={1，2，3，4，-1}，
∴∁U（A∪B）={4}．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知函数y=f（x）对任意的x∈（-
，
）满足f′（x）cosx+f（x）sinx＞0（其中f′（x）是函数f（x）的导函数），则下列不等式成立的是（ ）
| π |
| 2 |
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、f(0)＞
| ||||||
D、f(0)＞2f(
|
△ABC中，若（a-acosB）sinB=（b-ccosC）sinA，则这个三角形是（ ）
| A、底角不等于45°的等腰三角形 |
| B、锐角不等于45°的直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
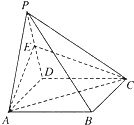如图，已知正三角形PAD，正方形ABCD，平面PAD⊥平面ABCD，E为PD的中点．